The models that describe our nonlinear phenomeana are defined through the language of mathematics. The equations representing the models may be ordinary differential equations (ODEs), or partial differential equations (PDEs). Moreover, some problems are described by ``algebraic'' equations, or by integral equations, or by some mixture. In addition to the differential equations there may be boundary conditions or initial conditions. Faced with the great variety of possible combinations and formats we basically restrict ourselves to the ODE situation. Many of the ideas and methods can be applied in a similar way to other equations.
1. A computer experiment
We define y1(t) and y2(t) to be functions that solve the system of two ODEs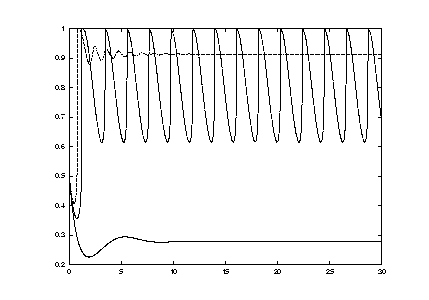
For the first series of experiments we take constant values of ![]() for each integration, but vary
for each integration, but vary ![]() from one integration to the next.
This treatment of the parameter
from one integration to the next.
This treatment of the parameter ![]() as being constant but variable is called quasistationary variation.
In Figure 1 we observe the results for three selected values of
as being constant but variable is called quasistationary variation.
In Figure 1 we observe the results for three selected values of ![]() ,
namely
,
namely
![]() ,
,
![]() ,
and
,
and
![]() .
For example, take
.
For example, take
![]() :
We observe that after a transient phase of, say,
:
We observe that after a transient phase of, say,
![]() ,
the trajectory y1(t) becomes stationary -- that is, it is attracted by a state with a constant value.
For
,
the trajectory y1(t) becomes stationary -- that is, it is attracted by a state with a constant value.
For
![]() there is again a transient phase, after which the trajectory becomes periodic with large oscillations.
The stationary state, and the periodic state respectively attract the neighboring trajectory.
Both attracting states are regular in shape.
Finally, for
there is again a transient phase, after which the trajectory becomes periodic with large oscillations.
The stationary state, and the periodic state respectively attract the neighboring trajectory.
Both attracting states are regular in shape.
Finally, for
![]() the attractor is again stationary, but now on a higher level.
The experiment has shown that the level and the quality of solutions vary with the parameter.
the attractor is again stationary, but now on a higher level.
The experiment has shown that the level and the quality of solutions vary with the parameter.
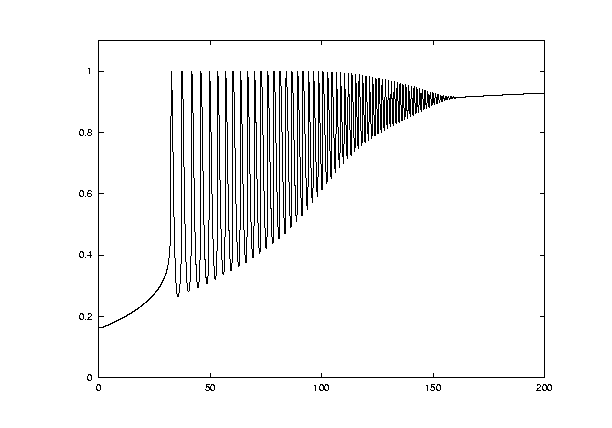
In a second type of experiment we let the parameter drift slowly in a nonstationary way,
![]() .
In order to move with the parameter through a range that matches the first set of experiments, we chose the additional differential equation
.
In order to move with the parameter through a range that matches the first set of experiments, we chose the additional differential equation
2. The model problem
We assume that our biological, physical, technical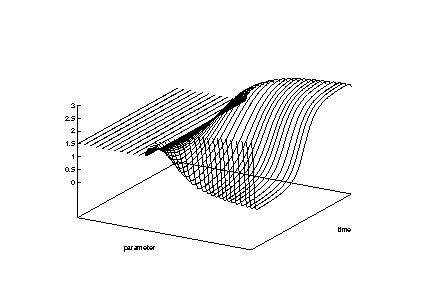
3. An example from chemistry
As an example consider WOBexd6, a chemical reaction with autocatalytic step
Looking back at Figure 2 we may notice that the phenomenon taking place for
![]()
![]() is of that kind.
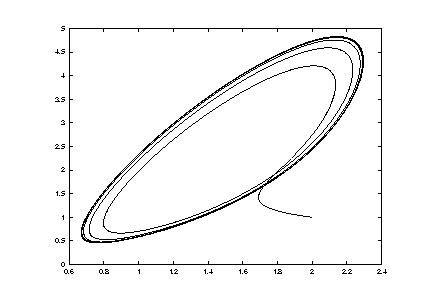
Here, in the quasistationary setting of Eq.(3), the attractors come out most regularly, as in Figure 3.
is of that kind.
Here, in the quasistationary setting of Eq.(3), the attractors come out most regularly, as in Figure 3.
The implicit function theorem (see any textbook of analysis) specifies sufficient criteria guaranteeing that a branch can be parameterized by ![]() .
For a specific stationary solution
.
For a specific stationary solution
![]() of Eq.(2) the criterion basically requires nonsingularity of the Jacobian matrix
of Eq.(2) the criterion basically requires nonsingularity of the Jacobian matrix
![]() .
Then there is an interval around
.
Then there is an interval around ![]() such that for all
such that for all ![]() in that interval Eq.(2) has a solution
in that interval Eq.(2) has a solution
![]() close to
close to
![]() .
.
5. An example from electrical engineering
The trigger circuit from WOBexa2 is described byFold bifurcations are frequently occurring in applications. For a boundary value problem (not of the type of Eq.(1)) see the Duffing oscillator WOBexb3, or the catalytic reaction WOBexb1, or the electric power system WOBexd15.
6. Bifurcation
Loosely speaking, a bifurcation with respect to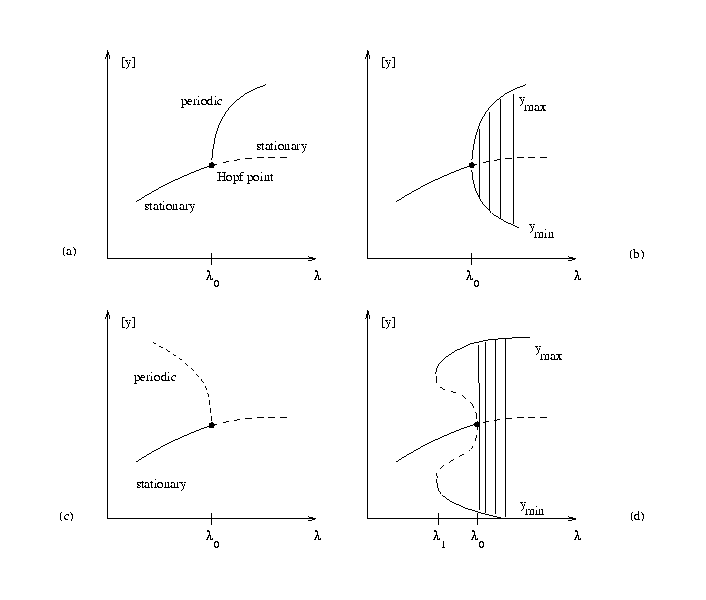
At a Hopf bifurcation, the branch of stationary solutions does not bifurcate; the Jacobian matrix
![]() is nonsingular. In Figure 7a, the
branch of stationary solutions extends beyond
is nonsingular. In Figure 7a, the
branch of stationary solutions extends beyond ![]() ,
but it is unstable for
,
but it is unstable for
![]() .
The Jacobian at a Hopf bifurcation has a pair of purely imaginary eigenvalues
.
The Jacobian at a Hopf bifurcation has a pair of purely imaginary eigenvalues
![]() .
Here a branch of periodic orbits is born. In Figure 7a, for
.
Here a branch of periodic orbits is born. In Figure 7a, for
![]() ,
,
![]() the periodic solutions merge into the stationary branch, the amplitude vanishes. The bifurcation is vertical, and the amplitude locally behaves like
the periodic solutions merge into the stationary branch, the amplitude vanishes. The bifurcation is vertical, and the amplitude locally behaves like
![]() .
This is seen in Figure 3, just concentrate on the y1-values belonging to the minimum t-value. The vertical axes in Figure 7 depict a scalar measure of the solutions, such as
.
This is seen in Figure 3, just concentrate on the y1-values belonging to the minimum t-value. The vertical axes in Figure 7 depict a scalar measure of the solutions, such as
The situation of Figures 7a, 7b depicts a transition without jump: Passing ![]() when increasing
when increasing ![]() one experiences a soft loss of stability of the stationary state; the bifurcation is supercritical. In Figure 7c we illustrate a subcritical situation where locally no stable state exists on one side of
one experiences a soft loss of stability of the stationary state; the bifurcation is supercritical. In Figure 7c we illustrate a subcritical situation where locally no stable state exists on one side of ![]() (here for
(here for
![]() ). Globally, this local scenario of Figure 7c often extends to a different situation, see Figure 7d: The branch of unstable periodic orbits bends back, gaining stability at a turning point like situation. Consequently, when we increase
). Globally, this local scenario of Figure 7c often extends to a different situation, see Figure 7d: The branch of unstable periodic orbits bends back, gaining stability at a turning point like situation. Consequently, when we increase ![]() beyond the critical Hopf parameter value
beyond the critical Hopf parameter value ![]() a jump occurs. For
a jump occurs. For
![]() in Figure 7d, there are no neighboring small-amplitude periodic solutions, and the dynamics is immediately attracted by a large-amplitude oscillation. This large jump is the hard loss of stability. Note that Figure 7d shows a bistable situation for
in Figure 7d, there are no neighboring small-amplitude periodic solutions, and the dynamics is immediately attracted by a large-amplitude oscillation. This large jump is the hard loss of stability. Note that Figure 7d shows a bistable situation for
![]() .
Note further that the described scenarios may also happen for decreasing
.
Note further that the described scenarios may also happen for decreasing ![]() .
.
Examples for a hard loss of stability are the computer experiment (WOBexd2), the bogie model (WOBexd10), the nerve model WOBexd14, and the power system WOBexd15. Examples for a soft loss of stability are again the computer experiment (the ``right'' bifurcation), the Brusselator (WOBexd1), and the reaction of Eq.(3).
In any arbitrary example of the type of Eq.(1) one must expect the occurrence of a fold bifurcation, or of a Hopf bifurcation. There are other bifurcations which are less likely to be found in a general equation. But many equations involve some symmetry. Often the symmetry in the equations reflects the common situation that a model consists of two or more identical parts that are coupled. When two identical subsystems are suitably coupled, one can exchange their states by a simple reflection. The related symmetry is the Z2-symmetry. For equations with a Z2-symmetry the pitchfork bifurcation is common too.
For a Z2-pitchfork bifurcation, the emanating branch consists of solutions that lose their symmetry. This phenomenon is called symmetry breaking. Schematically, the related bifurcation diagrams resemble those of Figure 7 of the Hopf scenario; compare Figure 8. The two asymmetric half-branches can be identified because they are transformed into each other by the underlying reflection that describes the exchange of the states of the subsystem.
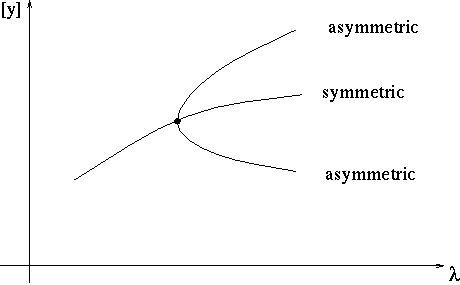
Examples of such pitchfork bifurcations are the Brusselator reaction WOBexa1, the flipflop WOBexa11, WOBexd1, the superconductivity WOBexb2, and the Duffing oscillator WOBexb3.
7. Period doubling and chaos
So far we have assumed solutions to Eq.(1) being regular in the sense stationary, or periodic. The deterministic system (1) allows for aperiodic solutions that have been named chaotic. There are several ways how to explain the onset of chaos. One of the most suggestive scenarios of chaos is tied to period doubling.
The local stability of a periodic orbit ![]() is determined by the eigenvalues of the monodromy matrix
is determined by the eigenvalues of the monodromy matrix
![]() where
where ![]() is the matrix function that solves the linear matrix initial-value problem
is the matrix function that solves the linear matrix initial-value problem
Dynamically, the period doubling bifurcation (or flip bifurcation) is the following scenario: Assume a branch of periodic solutions parameterized by ![]() with stable orbits on one side of
with stable orbits on one side of ![]() (say,
(say,
![]() )
and a multiplier crossing the unit circle with
)
and a multiplier crossing the unit circle with
![]() .
Then, locally, there are periodic orbits with the double period near
.
Then, locally, there are periodic orbits with the double period near ![]() .
These double-periodic orbits form a new branch that emerges at
.
These double-periodic orbits form a new branch that emerges at ![]() .
Note that the periods vary with
.
Note that the periods vary with ![]() ,
and the factor 2 of period doubling holds only asymptotically for
,
and the factor 2 of period doubling holds only asymptotically for
![]() .
The situation typically is as in the left part of Figure 9, for
.
The situation typically is as in the left part of Figure 9, for
![]() .
.
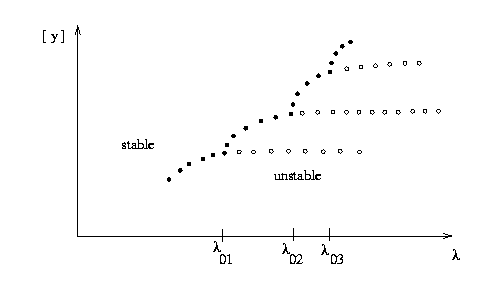
The ``new'' branch with the ``double'' period can experience a period doubling, too (in Figure 9, for
![]() ). There are many important applications were an infinite chain of such period doublings occurs for
). There are many important applications were an infinite chain of such period doublings occurs for
![]() ,
,
![]() ,
,
![]() ,
,
![]() In the supercritical case, the stability is exchanged to the branches of the double period. After some period doublings the period has become so large that the orbit looks irregular. As has been shown, the bifurcation values
In the supercritical case, the stability is exchanged to the branches of the double period. After some period doublings the period has become so large that the orbit looks irregular. As has been shown, the bifurcation values
![]() satisfy a universal scaling law,
satisfy a universal scaling law,
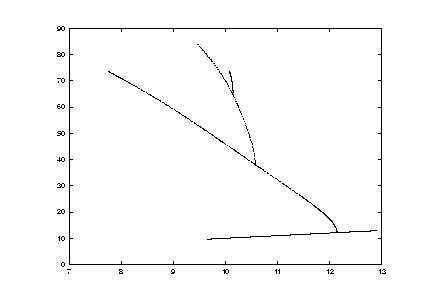
8. An example: isothermal reaction
An isothermal reaction (from [Smith et al., 1983], WOBexd13) is modelled by
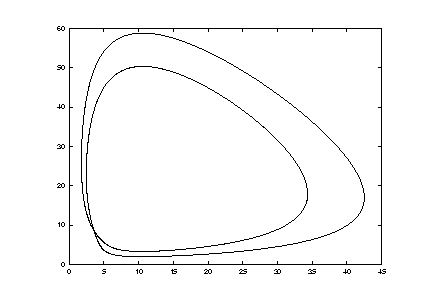
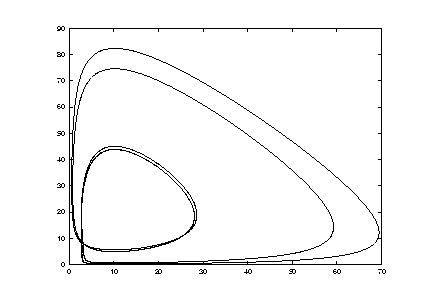
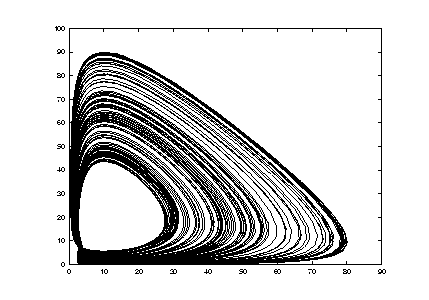
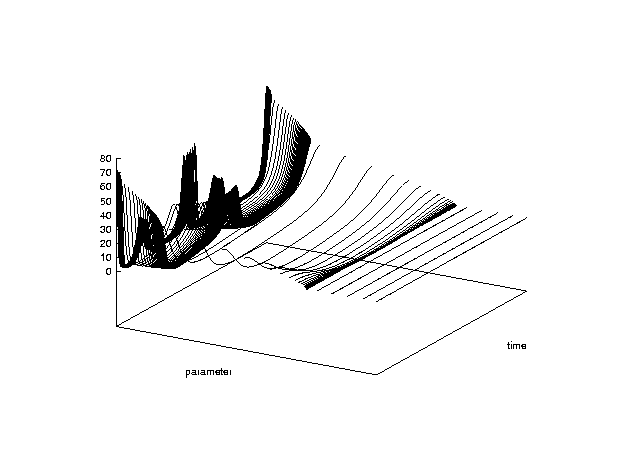
9. Other bifurcations
So far we have introduced three bifurcation mechanisms, namely turning point (fold bifurcation), Hopf bifurcation, and period doubling (flip bifurcation). These three bifurcations are the most important ones for a problem of the type of Eq.(1), because they occur most frequently in applications. There are other bifurcation phenomena which we briefly list.
First we return to the pitchfork. The simplest equation with pitchfork is
![]() .
The simplest equations exhibiting a certain phenomenon are called normal forms. As mentioned above, in case the underlying equation supports a Z2-symmetry, the pitchfork scenario is also likely to occur. The geometrical analogy of a pitchfork illustration with that of a Hopf bifurcation is no coincidence since the normal form of Hopf bifurcation is (in polar coordinates
.
The simplest equations exhibiting a certain phenomenon are called normal forms. As mentioned above, in case the underlying equation supports a Z2-symmetry, the pitchfork scenario is also likely to occur. The geometrical analogy of a pitchfork illustration with that of a Hopf bifurcation is no coincidence since the normal form of Hopf bifurcation is (in polar coordinates ![]() ,
,
![]() )
)
Branches of periodic orbits can show more bifurcation phenomena than just period doubling. The multipliers can cross the unit circle of the complex plane at +1. Then we encounter, for example, a turning point, or a pitchfork bifurcation. The turning point of periodic orbits is sometimes called cyclic fold bifurcation. When the crossing is with nonzero imaginary part, there is a bifurcation into a torus-like object.
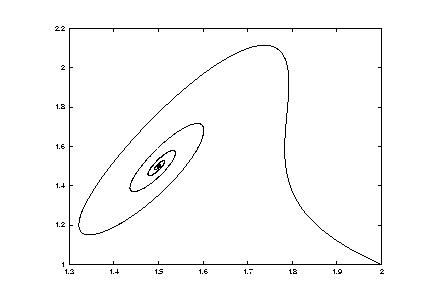
Periodic orbits are born in a Hopf bifurcation, and may end in a homoclinic orbit. To explain the simplest such scenario imagine in a plane a stationary state of saddle type. This saddle has a pair of entering trajectories and a pair of leaving trajectories. In case the leaving trajectory bends back such that it is identical with the entering trajectory we have a loop with infinite period. This is a homoclinic orbit. A periodic stable orbit close to a saddle is depicted in the phase portrait of Figure 14. Assume this is the situation for
![]() ,
and the periodic orbit and the saddle approach each other for
,
and the periodic orbit and the saddle approach each other for
![]() .
Then we encounter a homoclinic orbit for
.
Then we encounter a homoclinic orbit for ![]() and no periodic orbit for
and no periodic orbit for
![]() .
.
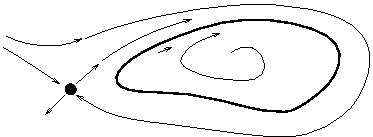
This simplest scenario of a homoclinic orbit illustrates how an unstable stationary state annihilates a periodic orbit. Analog phenomena are also possible with other unstable states. For example, a collision of an unstable periodic orbit might terminate a chaotic attractor. Generally, unstable states play a fundamental role in organizing dynamical behavior. This situation stresses the importance of calculating also unstable states. An example of the decisive role an unstable state plays in ``killing'' the operating regime is provided by models of voltage collapse, see WOBexd15.
10. Multi-parameter problems
The problems discussed so far depend on one real parameter
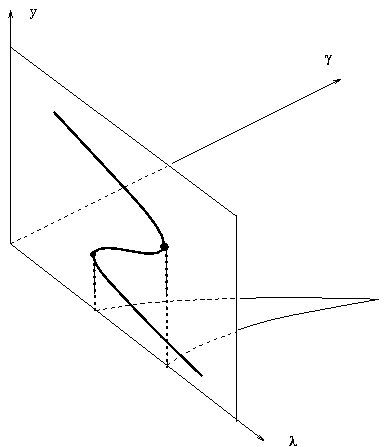
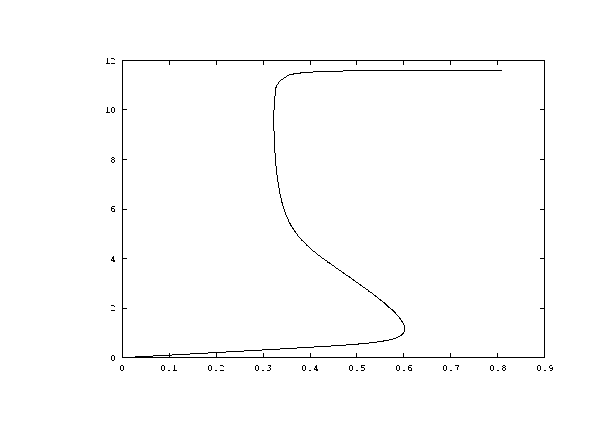
As a simple example, imagine a hysteresis situation as depicted in Figure 6. The range of bistability between the values ![]() of the two turning points may shrink when a second parameter
of the two turning points may shrink when a second parameter ![]() is varied, see Figure 15. Denote
is varied, see Figure 15. Denote ![]() the specific value where both
the specific value where both ![]() -values coincide. Then, on one side of
-values coincide. Then, on one side of ![]() (say for
(say for
![]() )
a bistable situation with jump phenomena exists whereas on the other side no bistability, and no bifurcation of that kind exists. Exactly
for
)
a bistable situation with jump phenomena exists whereas on the other side no bistability, and no bifurcation of that kind exists. Exactly
for
![]() the bifurcation is a hysteresis point, the two adjacent turning points have collapsed into a point of inflection. The value
the bifurcation is a hysteresis point, the two adjacent turning points have collapsed into a point of inflection. The value ![]() is seen as an organizing center separating two completely different dynamical situations. This is illustrated by the parameter chart of Figure 16.
The figure depicts also a jump-free transition from one operation point in the parameter plane to another.
A related example is provided by a catalytic reaction (WOBexb1).
The knowledge of the bifurcation curves allows to find easily a curve of parameter combinations
is seen as an organizing center separating two completely different dynamical situations. This is illustrated by the parameter chart of Figure 16.
The figure depicts also a jump-free transition from one operation point in the parameter plane to another.
A related example is provided by a catalytic reaction (WOBexb1).
The knowledge of the bifurcation curves allows to find easily a curve of parameter combinations
![]() that detours and avoids the jumps triggered by turning points.
that detours and avoids the jumps triggered by turning points.
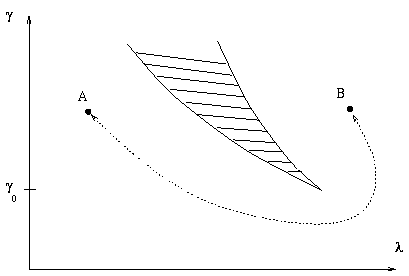
If in addition to ![]() and
and ![]() ,
a third parameter is considered to be freely variable, the bifurcation curves in the parameter plane extend to bifurcation surfaces in the parameter space. Possible bifurcation scenarios become even more involved. A theory of singularites has been established to analyze related higher-order bifurcations [Golubitsky & Schaeffer, 1985].
,
a third parameter is considered to be freely variable, the bifurcation curves in the parameter plane extend to bifurcation surfaces in the parameter space. Possible bifurcation scenarios become even more involved. A theory of singularites has been established to analyze related higher-order bifurcations [Golubitsky & Schaeffer, 1985].
11. Other problems
The model problem in Eq.(1) is a representative of a huge class of applications. But there are other problems equally important, and not covered by Eq.(1). For example, many classical oscillation problems are non-autonomous, such as12. Historical and bibliographical remarks
Early studies of nonlinearity include Euler's buckling problem [1744], and the work of Poincaré [1885]. Classical experimental studies were performed for fluid flow by Bénard [1901], and Taylor [1923]. Analytical investigations are numerous; we mention Liapunov's work on stability [1892], the studies of Andonov and coworkers on ``Hopf bifurcation'' in the 1930s [1987], Hopf's general theorem [1942], Rayleigh's analysis of convection [1916], and the book by Arnol'd on geometrical methods [1983]. Since the advent of powerful computers and algorithms the field has grown dramatically. The literature is rich, and here is not the space to present a survey. An elementary text book with many examples and practical hints is [Seydel, 1994]. Other texts are oriented more analytically. We mention a few examples, [Guckenheimer & Holmes, 1983], [Arrowsmith & Place, 1990], [Golubitsky & Schaeffer, 1985], [Chow & Hale, 1982], on Hopf bifurcation [Hassard et al., 1981], and on the chaos-oriented side, [Devaney, 1986], [Marek & Schreiber, 1991], [Schuster, 1984].References
Andronov, A.A., Vitt, A.A. & Khaikin, S.E. [1987] Theory of Oscillators (Dover Publications, New York).Arnol'd, V.I. [1983] Geometrical Methods in the Theory of Ordinary Differential Equations (Springer, New York).
Arrowsmith, D.K. & Place, C.M. [1990] An Introduction to Dynamical Systems (Cambridge University Press, Cambridge).
Bénard, H. [1901] ``Les tourbillons cellulaires dans une nappe liquide transportant de la chaleur par convection en regime permanent," Ann. Chim. Phys. 7, Ser. 23, p. 62.
Chow, S.-N. & Hale, J.K. [1982] Methods of Bifurcation Theory (Springer, New York).
Devaney, R.L. [1986] An Introduction to Chaotic Dynamical Systems (Menlo Park, Benjamin).
Euler, L. [1744] ``De Curvis Elasticis, Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes. Additamentum I. ," in Opera Omnia I Vol.24, 231-297, Zürich 1952.
Golubitsky, M. & Schaeffer, D.G. [1985] Singularities and Groups in Bifurcation Theory. Vol.1 (Springer, New York).
Guckenheimer, J. & Holmes, Ph. [1983] Nonlinear Oscillations, Dynamical Systems and Bifurcation of Vector Fields (Springer, New York).
Hassard, B.D., Kazarinoff, N.D., Wan, Y.-H. [1981] ``Theory and Applications of Hopf Bifurcation (Cambridge University Press).
Holodniok, M. & Kubícek, M. [1984] ``DERPER--an algorithm for the continuation of periodic solutions in ordinary differential equations," J. Comput. Phys. 55, 254-267.
Hopf, E. [1942] ``Abzweigung einer periodischen Lösung von einer stationären Lösung eines Differentialsystems," (Bericht der Math.-Phys. Klasse der Sächsischen Akademie der Wissenschaften zu Leipzig 94).
Krug, H.-J. & Kuhnert, L. [1985] `` Ein oszillierendes Modellsystem mit autokatalytischem Teilschritt," Z. Phys. Chemie 266, 65-73.
Liapunov, A.M. [1892] Stability of Motion (Academic Press, New York, 1966).
Marek, M. & Schreiber, I. [1991] Chaotic Behaviour of Deterministic Dissipative Systems. Cambridge University Press
Poincaré, H. [1885] ``Sur l'équilibre d'une masse fluide animée d'un mouvement de rotation," Acta Mathematica 7, 259-380.
Pönisch, G. & Schwetlick, H. [1982] ``Ein lokal überlinear konvergentes Verfahren zur Bestimmung von Rückkehrpunkten implizit definierter Raumkurven," Numer. Math. 38, 455-465.
Lord Rayleigh [1916] ``On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side," Philos. Mag. 32, 529-546.
Schuster, H.G. [1984] Deterministic Chaos (Physik-Verlag, Weinheim).
Seydel, R. [1994] Practical Bifurcation and Stability Analysis. From Equilibrium to Chaos. Second Edition. Springer Interdisciplinary Applied Mathematics, Vol. 5. (Springer, New York).
Smith, C.B., Kuszta, B., Lyberatos, G. & Bailey, J.E. [1983] ``Period doubling and complex dynamics in an isothermal chemical reaction system," Chem. Eng. Sci. 38, 425-430.
Taylor, G.I. [1923] ``Stability of a viscous liquid contained between two rotating cylinders," Philos. Trans. Roy. Soc. London A 223, 289-343.