CSTR
exd2
Model of a
continuous stirred tank reactor
(CSTR).
Variables and parameters:
Da: Damköhler number (bifurcation parameter: 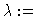 Da)
y1 , y2: describe the material and
energy balances
Da)
y1 , y2: describe the material and
energy balances
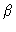 :
the heat transfer coefficient
:
the heat transfer coefficient 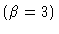 B: the rise in adiabatic temperature (B=16.2)
B: the rise in adiabatic temperature (B=16.2)
CSTR model equations:
Figure 1
Branching diagram y1(0) versus Da. One branch of stationary solutions, and two branches of periodic orbits branching off at two Hopf bifurcations.
Figure 2
y1(t) simulation for
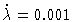 ,
,
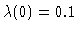 ,
,
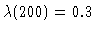 with initial values
y1(0)=0.1644,
y2(0)=0.6658
with initial values
y1(0)=0.1644,
y2(0)=0.6658
Figure 3
y1(t) simulation for
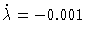 ,
,
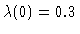 ,
,
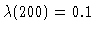 with initial values
y1(0)=0.9279,
y2(0)=3.76
with initial values
y1(0)=0.9279,
y2(0)=3.76
Postscript-Files for better printing results:
This Example
Figure 1
Figure 2
Figure 3
![]() ,
,
![]() ,
,
![]() with initial values
y1(0)=0.1644,
y2(0)=0.6658
with initial values
y1(0)=0.1644,
y2(0)=0.6658
![]() ,
,
![]() ,
,
![]() with initial values
y1(0)=0.9279,
y2(0)=3.76
with initial values
y1(0)=0.9279,
y2(0)=3.76