Chemical Reaction with Autocatalytic Step

exd6
Variables and parameters:

yi(t): concentrations of chemicals

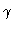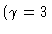$\gamma$: flow $(\gamma=3$)

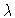$\lambda$: velocity coefficient of autocatalytic step (bifurcation parameter)


Model equations:

\begin{displaymath}\dot y_1 & = \gamma - y_1 - \lambda y_1 y_3 \cr\end{displaymath}


\begin{displaymath}\dot y_2 & = y_1 - y_2 y_3 \cr\end{displaymath}


\begin{displaymath}\dot y_3 & = y_2 y_3 - \lambda y_1 y_3 \cr\end{displaymath}



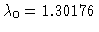Hopf Bifurcation at $\lambda_0=1.30176$ with initial period T0=6.03555

Comments

Figure 1
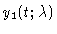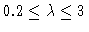Stable solutions, $y_1(t;\lambda)$ for $0.2\le \lambda\le 3$; the time is normalized to unity. Stationary and periodic orbits meet in a Hopf bifurcation.

Figure 2
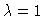$\lambda=1$, projection to the (y1,y2) plane. Initial values: y1=2, y2=y3=1. Dynamics of a stable focus.

Figure 3
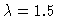$\lambda=1.5$, projection to the (y1,y2) plane. Initial values: y1=2, y2=y3=1. Dynamics of a stable limit cycle.

Figure 4
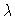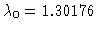Bifurcation diagram y1(0) versus $\lambda$; Hopf bifurcation at $\lambda_0=1.30176$.

Postscript-Files for better printing results:

This Example
Figure 1
Figure 2
Figure 3
Figure 4