WOB

Superconductivity Within a Slab

exb2

Model of a superconducting slab in a parallel magnetic field.

Variables and parameters:

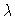$\lambda$ : square of external field (bifurcation parameter)

d: thickness of the slab (d=5)

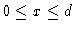
x: space variable, $0\le x\le d$

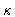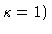
$\kappa$ : Ginzburg-Landau parameter ( $\kappa=1)$

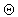$\Theta$ : an order parameter characterizing different superconducting states

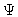$\Psi$ : potential of the magnetic field

The Ginzburg-Landau equations are equivalent to the boundary-value problem of two second-order ODEs

$\begin{displaymath}\Theta'' & = \Theta(\Theta^2 -1+\lambda \Psi^2 )\kappa^2 \cr\end{displaymath}$

$\begin{displaymath}\Psi''& = \Theta^2 \Psi \cr\end{displaymath}$

$\begin{displaymath}\Theta'(0) = \Theta'(d) = 0, \ \ \Psi '(0) = \Psi '(d) = 1.\end{displaymath}$

Figure 1
Bifurcation diagram 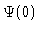$\Psi(0)$ versus 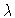$\lambda$ . Two branches intersecting in a pitchfork bifurcation.

Figure 2
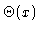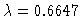Two antisymmetric solutions $\Theta(x)$ for $\lambda=0.6647$ .

Figure 3
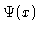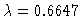Two antisymmetric solutions $\Psi(x)$ for $\lambda=0.6647$ .

Figure 4
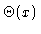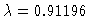Symmetric solution $\Theta(x)$ for $\lambda=0.91196$ .

Figure 5
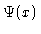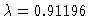Symmetric solution $\Psi(x)$ for $\lambda=0.91196$ .