Catalytic Reaction in a Flat Particle
exb1
Variables and parameters:
y: dimensionless concentration
x: dimensionless coordinate (
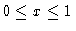 )
)
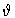 :
Thiele modulus (bifurcation parameter:
:
Thiele modulus (bifurcation parameter:
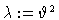 )
)
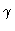 :
dimensionless energy of activation
:
dimensionless energy of activation
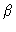 :
dimensionless parameter of heat evolution,
:
dimensionless parameter of heat evolution, 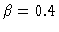
ODE boundary-value problem
We choose the
first-order reaction (m=1).
Figure 1
Branching diagrams y1(0) versus 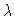 for six values of the second parameter
for six values of the second parameter 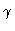 :
:
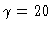 (left profile),
(left profile), 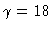 ,
14, 12, and
,
14, 12, and 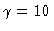 (right profile).
(right profile).
Figure 2
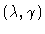 -parameter chart with two turning point curves.
-parameter chart with two turning point curves.
Postscript-Files for better printing results:
This Example
Figure 1
Figure 2
![]() -parameter chart with two turning point curves.
-parameter chart with two turning point curves.