Hodgkin-Huxley Nerve Model

exd14
Variables and parameters:

U (t): membrane potential of a nerve cell

V1, V2,V3: artificial variables defining permeability of the membrane

Ia: applied current ( $\lambda:=I_a$ bifurcation parameter)

\begin{displaymath}I_a &=\dot U+36 V_1^4(U-12) +120 V_2^3V_3 (U+115)+0.3(U+10.613),\cr\end{displaymath}


\begin{displaymath}\dot V_i &=\alpha_i(U)(1-V_i)-\beta_i(U)V_i,\quad i=1,2,3.\cr\end{displaymath}



transfer rates:

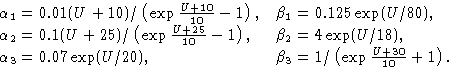
\begin{displaymath}\matrix{\alpha_1 =0.01 (U+10)/\left(\exp{U+10\over 10}-1\righ... ...hfill & \beta_3 =1/\left(\exp{U+30\over 10}+1\right).\hfill\cr}\end{displaymath}


Comments

Figure 1
(U,V1)-phase diagram of the Hodgkin-Huxley equation; two trajectories: U(0)=-5 and -6, with V1(0)=0.31, V2(0)=0.05, V3(0)=0.6 and Ia=0.

Figure 2
U(t) for $0\leq t\leq 30$; Hodgkin-Huxley equation; two trajectories: U(0)=-5 and -6, with V1(0)=0.31, V2(0)=0.05, V3(0)=0.6 and Ia=0.

Figure 3
(U,V1)-phase diagram of the Hodgkin-Huxley equation; trajectory approaching a limit cycle. U(0)=-5, V1(0)=0.31, V2(0)=0.05, V3(0)=0.6 and Ia=-10.


Figure 4
(U,V1)-phase diagram of the Hodgkin-Huxley equation; six trajectories U(0)=U0, with V1(0)=0.31, V2(0)=0.05, V3(0)=0.6 and Ia=0; U0=-5.0/-5.2/-5.4/-5.6/-5.8/-6.0

Figure 5
U(t) for $0\leq t\leq 30$; membrane potential of the Hodgkin-Huxley equation; six trajectories U(0)=U0, with V1(0)=0.31, V2(0)=0.05, V3(0)=0.6 and Ia=0; U0=-5.0/-5.2/-5.4/-5.6/-5.8/-6.0

Postscript-Files for better printing results:

This Example
Figure 1
Figure 2
Figure 3
Figure 4
Figure 5