Computational Bifurcation

As seen in Tutorial 3, the calculated branch consists of a chain of discrete solutions. It is most unlikely that the continuation happens to hit a bifurcation exactly. Rather a bifurcation will be hidden in the space between the calculated solutions. Hence the first task of a computational bifurcation analysis is to (A) detect a bifurcation point.

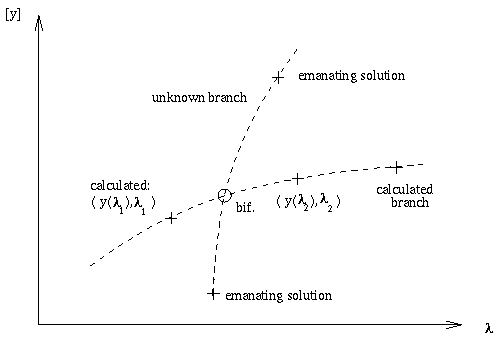
The minimum requirement is to straddle the bifurcation--that is, to calculate one solution on either ``side." This information can be easily condensed to a rough approximation to the bifurcation. For some applications it is necessary to (B) calculate the bifurcation point accurately.

After having carried out steps (A) and (B), enough data may be available to (C) determine the type of bifurcation.

Depending on the type of bifurcation, a new branch may bifurcate off distinct from the branch that was calculated during the continuation. Then the completing step is to (D) switch branches.

Branch switching amounts to calculating one solution on each emanating branch. This ``first'' solution provides information on the quality of the solutions on that new branch, and on its direction. The four basic tasks of the computation of bifurcation points are summarized in Fig. 1.

Fig. 1. Branch switching.

A qualitative bifurcation analysis involves even more tasks. For example, the linear stability of at least one solution on either side of a bifurcation needs to be tested. To obtain a more global picture, the approximate domain of attraction of a stable solution will be explored by selecting initial vectors in a larger neighborhood, and by integrating the initial-value problems until it becomes clear to which attractor the trajectory is approaching. This kind of expensive exploration by simulation frequently will be based on a trial-and-error-basis. The final aim is to explore the diameter of the domain of attraction to get a feeling for the sensitivity of a stable solution. The question is, how large a perturbation of a stable solution is allowed to be such that the response to the perturbation decays to zero.

Naturally, the various kinds of bifurcation have required to develop various different solution strategies to the above-mentioned tasks. This tutorial cannot present an exhaustive survey. Instead we explain ideas that have successfully been adapted to various bifurcation scenarios. In the first part of this tutorial we concentrate on the formally simplest equation,

$${\bf f}({\bf y},\lambda)=\00,\eqno(1)$$

which may represent stationary solutions of a system of ordinary differential equations. Later, we shall proceed to periodic solutions of ordinary differential equations.

2.    Bifurcation test functions

Bifurcation test functions provide the framework for procedures designed to detect bifurcations. Such a test function $\tau({\bf y},\lambda)$ is evaluated along a branch during continuation. The basic feature of a test function for detecting a bifurcation $({\bf y}_0,\lambda_0)$ is $\tau({\bf y}_0,\lambda_0)=0$. That is to say, the bifurcation is a zero of the test function. Moreover, we require $\tau$ to be continuous in a neighborhood of $({\bf y}_0,\lambda_0)$, and to change sign. With such a test function at hand, the remaining exercise is to detect zeros of $\tau$ during branch tracing. By interpolation based on the discrete values $\tau_j,\tau_{j+1}, \ldots$ an approximation to a zero $\lambda_0$ is calculated (see Fig. 2). This also solves the task (B), when the continuation step length is sufficiently short. Methods of inverse interpolation, or root finding algorithms can be used to approximate $\lambda_0$. Related procedures that exploit the continuation output to approximate bifurcations are called indirect methods.

Fig. 2. Application of a test function $\tau$.

The simplest example of a test function is available for the stationary-state Eq.(1). In case in $({\bf y}_0,\lambda_0)$ two branches of stationary solutions meet, by the implicit function theorem, the Jacobian matrix ${\bf f}_{\bf y}({\bf y}_0 ,\lambda_0)$ is singular. Hence

$$\tau ({\bf y},\lambda ): = \det {\bf f}_{\bf y}({\bf y},\lambda) \eqno{(2)}$$

is a natural candidate for such bifurcations. This test function can be easily calculated when the Jacobian was decomposed into a ${\bf L}{\bf U}$ decomposition

$${\bf P}{\bf f}_{{\bf y}}={\bf L}{\bf U},$$

which results in

$$\tau=\det({\bf P})\det({\bf U})=\pm u_{11}\cdot\ldots\cdot u_{nn}.$$

Here ${\bf P}$ is the permutation matrix that accounts for partial pivoting, ${\bf L}$ is lower triangular with l_ii=1, and $u_{ii}, \ i=1,\ldots,n$, are the diagonal entries of the upper triangular matrix ${\bf U}$. The test function of Eq.(2) is not scaling invariant, which may lead to difficulties in deciding whether $\tau$ is ``large'', or ``small.'' The test function of Eq.(2) is not relevant for Hopf bifurcation.

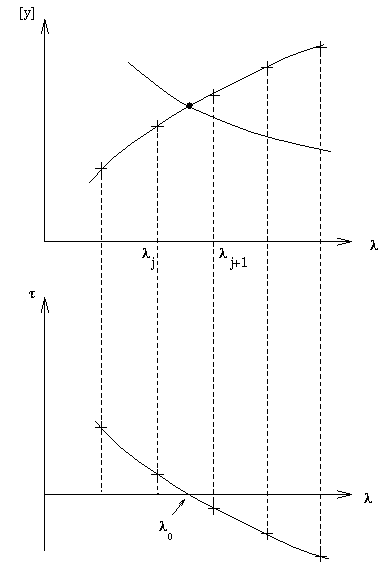
There are other test functions. In case the eigenvalues $\mu_1 ,\ldots ,\mu_n$ of the Jacobian matrices are calculated, with $\mu_k =\alpha_k +i\beta_k$ and i denoting the imaginary unit, the test function

$$\tau : = \max \{ \alpha_1 ,\ldots , \alpha_n\} \eqno{(3)}$$

indicates stability. This test function detects those bifurcations that separate stable from unstable solutions. Another test function will be defined below (in Eq.(7)).

Detecting turning points is much easier, and can be based on geometrical arguments exploiting ${d \lambda \over d y}=0$. Several strategies of obtaining approximations to turning points are suggested in [Seydel, 1994].

3.     Direct computation of bifurcations

The idea of a direct method for calculating a bifurcation of ${\bf f}({\bf y},\lambda)=0$ is to set up an equation ${\bf F}({\bf y},\lambda)=\00$ which selectively and exclusively has a bifurcation $({\bf y}_0,\lambda_0)$ as solution. Then the solution procedure (Newton's method, for instance) applied to ${\bf F}({\bf y},\lambda)=\00$ provides an iteration to calculate $({\bf y}_0,\lambda_0)$. Basically, the equation consists of

$${\bf F}({\bf Y}): = {\bf F}({\bf y},\lambda ): = \pmatrix{{\b... ...({\bf y},\lambda) \cr \tau({\bf y},\lambda) \cr} =\00 \eqno(4)$$

with $\tau$ being a bifurcation test function. The choice of the test functions (2) or (3) in this context has not become popular because of the difficulty in obtaining the gradient $\nabla \tau$. But Eq.(4) fixes the idea, and illustrates that ${\bf F}$ typically is an enlargement of ${\bf f}$. An equation as Eq.(4) consisting of n+1 scalar equations for $({\bf y}_0,\lambda_0)$ is called a minimal extended system for calculating a bifurcation point.

A basic approach related to test function (3) attaches the linearization, and characterizes $({\bf y}_0,\lambda_0)$ by a Jacobian ${\bf f}_{\bf y}$ having a zero eigenvalue with eigenvector ${\bf h}$. The resulting branching system from [Seydel, 1977, 1979c]

$${\bf F}({\bf y},\lambda,{\bf h}):=\pmatrix {{\bf f}({\bf y},\... ...f f}_{\bf y}({\bf y},\lambda){\bf h}\cr h_k - 1} =\00 \eqno(5)$$

has the dimension 2n+1. For moderate values of n, a direct solution of (5) by Newton-type methods is straightforward (``call SOLVER"). This system has served as nucleus for several direct methods. Special implementations exploiting the block structure have been suggested [Moore & Spence, 1980], [Doedel, 1997], which are essential for large values of n.

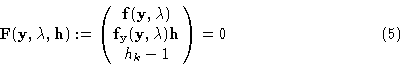
The solution of the branching system of Eq.(5) includes ${\bf y}_0$, $\lambda_0$, and the right eigenvector ${\bf h}_0$. This vector ${\bf h}_0$ can be embedded into a continuous family of vectors ${\bf h}$ defined also for solutions $({\bf y},\lambda)$ different from $({\bf y}_0,\lambda_0)$. This generalized ${\bf h}={\bf h}({\bf y},\lambda)$, which satisfies

$${\bf h}_0={\bf h}({\bf y}_0,\lambda_0),$$

is defined by

$$[({\bf I}-{\bf e}_l {\bf e}^{\everymath{\scriptstyle}\everydi... ...yle}\everydisplay{\textstyle}}_k ]{\bf h}= {\bf e}_l .\eqno(6)$$

The defect of ${\bf f}_{\bf y}({\bf y},\lambda){\bf h}$ gives rise to a new test function,

$$\tau_{lk} ({\bf y},\lambda ): = {\bf e}^{\everymath{\scriptst... ...extstyle}}_l{\bf f}_{\bf y}({\bf y},\lambda ){\bf h}. \eqno(7)$$

The test function (7) for suitably chosen indices l, k (such that $h_k\ne 0$, $g_l\ne 0$ where ${\bf g}$ is the left eigenvector of ${\bf f}_{\bf y}({\bf y}_0 ,\lambda_0)$) qualifies to detect singularities of the Jacobian [Seydel 1977, 1979a, 1979c, 1991, 1997a]. For this test function an efficient way of evaluating $\nabla \tau$ was found [Griewank & Reddien, 1984], which suggests to use $\tau$ from Eq.(7) in connection with the minimal extended system (4).

The branching system (5) has a nonsingular Jacobian in case of turning points ( ${\bf f}_\lambda\not\in\hbox{range}({\bf f}_{\bf y})$). But the Jacobian is singular in case of bifurcation points with ${\bf f}_\lambda\in\hbox{range}({\bf f}_{\bf y})$. This may badly affect the convergence of iterative methods. To remove the singularity, the problem can be reformulated as a turning point problem. The idea is to perturb the equation by something that is zero in the bifurcation [Moore, 1980],

$$\tilde{\bf f}({\bf y},\lambda ,\tilde\lambda ): = {\bf f}({\bf y},\lambda ) + \tilde \lambda {\bf r}, \eqno(8)$$

for a parameter $\tilde\lambda$ and a vector ${\bf r}$ that satisfies ${\bf r}\notin \hbox { range } ({\bf f}_{\bf y}({\bf y}_0 ,\lambda_0) \vert {\bf f}_\lambda ({\bf y}_0 ,\lambda_0)).$ One considers $\tilde\lambda$ a new branching parameter and sets $\tilde {\bf y}:=({\bf y},\lambda)$. For the modified function $\tilde{\bf f}$

$$\partial \tilde {\bf f}/\partial \tilde\lambda = {\bf r}\not\... ...ox { range } (\partial \tilde {\bf f}/\partial \tilde {\bf y})$$

holds. Hence, the bifurcation point of ${\bf f}({\bf y},\lambda )=\00$ has become a turning point of $\tilde {\bf f}( \tilde {\bf y},\tilde\lambda )=\00$ for $\tilde\lambda=0$. Because this modified equation has a rectangular Jacobian with n rows and n+1 columns, its singularity is characterized by the existence of a left eigenvector ${\bf g}$ for the eigenvalue 0, rather than the right eigenvector ${\bf h}$ in Eq.(5). The related eigenvalue equation $\00 = {\bf g}\hbox{{$^t$ }\hbox to 3.0pt{\hss $^r$ }}\tilde {\bf f}_{\tilde{\bf y}}$ leads to the system

$$\pmatrix {{\bf f}({\bf y},\lambda ) + \tilde\lambda {\bf r}\c... ...$}\hbox to 3.0pt{\hss $^r$}}{\bf r}- 1 \cr } = \00 \ ;\eqno (9)$$

Moore chooses ${\bf r}= {\bf g}$.

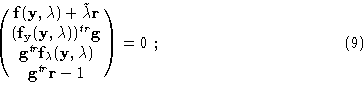
For Hopf bifurcation points, the branching system analog to (5) for the complex-conjugate eigenvector ${\bf h}={\bf h}^{Re}+i{\bf h}^{Im}$ of the eigenvalue $i\beta$ attaches ${\bf f}_{\bf y}{\bf h}=i\beta{\bf h}$. In real form this amounts to

$$\pmatrix {{\bf f}({\bf y},\lambda ) \cr {\bf f}_{\bf y}({\bf... ...bf h}^{Re} \cr h_k^{Re} - 1 \cr h^{Im}_k \cr }= \00. \eqno(10)$$

For this extended system of dimension 3n+2 again SOLVER can be called (if n is not too large), or special implementations can be applied that exploit the block structure [Griewank & Reddien, 1983], [Roose, 1985].

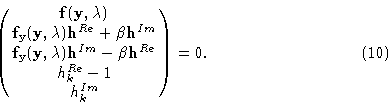
4.     ODE boundary-value problems

Analogous methods have been suggested for boundary-value problems. As a prototype equation, consider the two-point boundary-value problem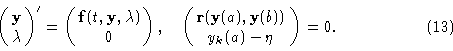

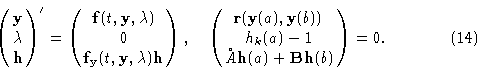
$${\bf y}' = {\bf f}(t,{\bf y},\lambda ),\quad {\bf r}({\bf y}(a),{\bf y}(b)) = \00,\eqno (11)$$

for $a\leq t\leq b$. The vector function ${\bf r}$ defines n boundary conditions. Similarly as in the finite-dimensional situation described above, various tasks of a computational bifurcation analysis can be formulated via suitable enlarged boundary-value problems of the general type

$${\bf Y}' = {\bf F}(t,{\bf Y}),\quad {\bf R}({\bf Y}(a),{\bf Y}(b)) = \00. \eqno (12)$$

As a simple example we take the local parameterization by y_k(a). Then Eq.(12) consists of n+1 differential equations and n+1 boundary conditions,

$$\pmatrix {{\bf y}\cr \lambda \cr}'= \pmatrix {{\bf f}(t, {\bf... ...bf y}(a), {\bf y}(b)) \cr y_k (a) - \eta \cr} = \00. \eqno (13)$$

The branching system for ODE boundary-value problems is

$$\pmatrix {{\bf y}\cr \lambda \cr {\bf h}\cr}'= \pmatrix {{\bf... ...1 \cr \AA {\bf h}(a) + {\bf B}{\bf h}(b) \cr} = \00. \eqno (14)$$

In this system of size 2n+1 the $n\times n$ matrices $\AA$ and ${\bf B}$ consist of the first-order derivatives of ${\bf r}$ with respect to ${\bf y}(a)$ and ${\bf y}(b)$. For an embedding of the vector ${\bf h}$, and for the definition of a test function, see [Seydel, 1977, 1979a, 1994].

5.     Branch switching

Branch switching is based on the predictor-corrector approach. It is essential to calculate a good initial guess to an emanating solution. Then this initial guess serves as predictor to trace the branch, see Tutorial 3.

One way of creating such a predictor is to accurately calculate the bifurcation, and the tangents to all branches that meet in $({\bf y}_0,\lambda_0)$, see [Keller, 1977]. For pitchfork bifurcations, the vector ${\bf h}_0$ from Eq.(5) serves as tangent along the branch perpendicular to the $\lambda$-axis. Then the predictor is given by

$$({\bf y}_0+\delta{\bf h}_0,\lambda_0)$$

for some $\delta\ne 0$. An accurate calculation of the bifurcation ( ${\bf y}_0,\lambda_0$) and of the vector ${\bf h}_0$ is not required because approximations can be easily obtained by interpolation. The right eigenvector ${\bf h}_0$ is approximated by interpolation based on the vectors ${\bf h}$ defined by Eq.(6). In an analogous way, the predictor for a periodic orbit close to a Hopf bifurcation can be obtained.

For the corrector, a good strategy is to set up selective equations that support convergence towards the new branch rather than convergence back to the known branch. This can be based on symmetry breaking.

6.     Symmetry

Since bifurcation is frequently tied to symmetry, or to symmetry breaking, it is natural to exploit symmetry also for computational purposes. Early papers applied symmetry to branch switching [Seydel, 1983], and to the solution of the branching system [Werner & Spence, 1984]. As suggested in the latter paper, the vectors ${\bf y}$ and ${\bf h}$ can be reduced to certain symmetric or anti-symmetric subspaces, which allows to reduce the size of the branching system from 2n+1 to n+1. In the former paper, special equations were formulated that are selective. That is, ideally, an equation allows only for a solution of a specific kind of asymmetry.

Because the situation is more complicated for boundary-value problems, we fix ideas for Eq.(11). To classify and investigate symmetries in the solution, consider a reflection $\tilde y_i (t) \hbox { of } y_i (t)$. We define the component y_i to be symmetric if

$$\tilde y_i (t) = y_i (t)$$

holds for all t in the interval $a\le t\le b$. We shall say that a boundary-value problem supports symmetry if it is solved by $\tilde {\bf y}$ whenever it is solved by ${\bf y}$. In particular, the following kinds of symmetries occur frequently in bifurcation problems:

$$& y_i(t) = \tilde y_i (t) \hbox { for }\qquad\tilde y_i (t):= y_i (a+b-t),&(15a) \cr$$

$$& y_i(t) = \tilde y_i(t) \hbox { for }\qquad \tilde y_i (t) := - y_i (a+b-t),&(15b) \cr$$

$$& y_i (t) = \tilde y_i (t) \hbox { for }\qquad\tilde y_i(t): = - y_i\pmatrix {t + {b-a \over 2}},&(15c) \cr$$

$$&y_i (t) = \tilde y_i (t) \hbox { for }\qquad \tilde y_i(t): = y_i \pmatrix{t + {b-a \over 2}}.&(15d) \cr$$

In Eq.(15a) the function y_i is even, in Eq.(15b) it is odd. Eqs.(15c,d) are characteristic for bifurcations of periodic solutions with period b-a. The latter type actually has a period ${1\over 2}(b-a)$, and is suitable for period doubling. A breaking of symmetry of an emanating solution is easily discovered, and the asymmetric branch can be parameterized by the size of asymmetry. The details are in [Seydel, 1983]. For example, in the situation of Eq.(15a), the asymmetric branch can be parameterized by its degree of asymmetry, $\gamma$, in a boundary condition

$$r_{n+1}:=y_k(b)-y_k(a)-\gamma,$$

that is used in Eq.(13), replacing the (n+1)st boundary condition.

Recently, symmetry-based algorithms have found some interest [Allgower et al., 1992], [Allgower et al., 1993].

7.     Periodic solutions

A class of differential equations with many applications are autonomous equations,

$$\dot{\bf y}={\bf f}({\bf y},\lambda).\eqno(16)$$

Periodic solutions ${\bf y}$ satisfy the boundary conditions

$${\bf y}(0)-{\bf y}(T)=\00\eqno(17)$$

for some minimum period T>0. To give t=0 a meaning, a phase condition $\phi({\bf y}(0),\lambda)=0$ is required. The equation $\phi({\bf y}(0),\lambda)=0$ defines a Poincaré surface for each $\lambda$. The orbit should intersect this surface transversally. That is, ${\bf f}({\bf y},\lambda)\hbox{{$^t$ }\hbox to 3.0pt{\hss $^r$ }}\phi_{\bf y}\ne 0$ should hold. There are several possibilities of phase conditions that can be prescribed on ${\bf y}(0)$. An example is

$$\phi({\bf y}(0),\lambda ): = y_k (0) - \eta = 0 \eqno(18a)$$

for some k and $\eta$ in the range of y_k(t). For transversality choose k such that $\vert\dot y_k\vert$ is maximal. Another phase condition is

$$\phi({\bf y}(0),\lambda ) := \dot y_k(0) = f_k ({\bf y}(0),\lambda) = 0,\eqno(18b)$$

here at ${\bf y}(0)$ the tangent to the orbit is orthogonal to the y_k-axis. A phase condition with built-in transversality is

$$\phi({\bf y}(0),\lambda):={\bf f}({\bf z},\lambda)\hbox{{$^t$}\hbox to 3.0pt{\hss $^r$}}({\bf y}(0)-{\bf z})=0.\eqno(18c)$$

In Eq.(18c), ${\bf z}$ is a point near the orbit, such as ${\bf z}=\hat{\bf y}(0)$ where $\hat{\bf y}(t)$ is some approximation or a solution of a previous continuation step, see [Beyn, 1990]. A frequently used phase condition is

$$\int^1_0 {\bf y}\hbox{{$^t$}\hbox to 3.0pt{\hss $^r$}}\dot {\bf z}\ dt =0,\eqno(19)$$

where ${\bf z}(t)$ is a calculated (previous) periodic solution, see [Doedel et al, 1991].

With a phase condition, the problem of calculating periodic solutions can be formulated as boundary-value problem. Defining $\tilde n:=n+1$ and

$$\tilde {\bf y}:= \pmatrix {{\bf y}\cr T \cr}, \ \ \tilde {\bf... ... - {\bf y}(1) \cr \phi ({\bf y}(0), \lambda) \cr} , \eqno (20a)$$

the calculation of periodic orbits mounts to solve the two-point boundary-value problem

$$\tilde {\bf y}' = \tilde {\bf f}(\tilde {\bf y},\lambda), \ \... ...\bf r} (\tilde {\bf y}(0),\tilde {\bf y}(1)) = \00. \eqno (20b)$$

Now the bifurcation methods for boundary-value problems can be applied to the bifurcation of periodic orbits. For example, the boundary-value problem counterpart to Eq.(10) for Hopf bifurcations is the branching system

$$\pmatrix {{\bf y}\cr T \cr \lambda \cr {\bf h}\cr}' = \pmatri... ...rtial f_1 / \partial y_i \cr h_1 (0) - 1 \cr} = \00. \eqno (21)$$

In the Hopf situation, it is more efficient to apply Eq.(10), which does not involve differential equations.

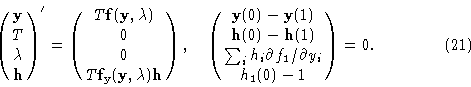
For period doubling, which is a bifurcation of period 2T solutions with symmetry breaking, the approach of Section 6 can be applied using Eq.(15d), with b=2T, a=0. If ${\bf z}$ is the emanating solution, the corresponding parameter $\gamma$ of asymmety is $\gamma= z_k(a)- z_k({a+b\over 2})=z_k(0)-z_k(T)$. The initial vector ${\bf h}(0)$ of the ${\bf h}$ that corresponds to the 2T period can be identified with the eigenvector that corresponds to the eigenvalue -1 of the monodromy matrix ${\bf M}$. Consequently, ${\bf h}(T)=-{\bf h}(0)$, and the interval of length 2T (or 2 in the normalization of Eq.(20)) can be reduced to the ``simple'' length T (or 1). Thus the branching system specializes in the period doubling case to

$$\pmatrix {{\bf y}\cr T \cr \lambda \cr {\bf h}\cr}' = \pmatri... ... {\bf h}(0) + {\bf h}(1) \cr h_k (0) - 1 \cr} = \00. \eqno (22)$$

For further references on the calculation of periodic orbits, see [Doedel et al., 1991], [Doedel, 1997], [Holodniok & Kubicek, 1984], [Reithmeier, 1991], [Seydel, 1981], and [Seydel, 1994].

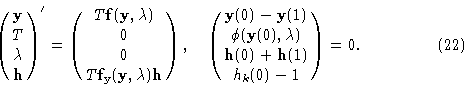
8.     Bifurcation curves

The essential advantage of the basic branching system (5) and its variants (9), (10), (14), (21), (22) compared to indirect methods is that such systems are most comfortably used to calculate bifurcation curves in two-parameter problems. Then, with ${\bf Y}=({\bf y},\lambda)$, N=n+1 (or ${\bf Y}=({\bf y},\lambda,{\bf h})$, N=2n+1 for Eq.(5)/(14), or ${\bf Y}=({\bf y},\lambda,{\bf h}^{Re},{\bf h}^{Im})$, N=3n+1 for Eq.(10)), and $\gamma$ denoting the second parameter, a bifurcation with respect to $\lambda$ is defined by an extended system of equations ${\bf F}({\bf Y},\gamma)=\00$. This system of N equations is a continuation problem. That is, with a branching system at hand, the problem of calculating a bifurcation curve is just a standard continuation problem. This is most practical, and basic for the inverse bifurcation problem, which is the question how to set a control parameter $\gamma$ such that a bifurcation in $\lambda$ is shifted to a desired range. The bifurcation curves separate the parameter domain into subdomains. Selecting one parameter combination $(\lambda,\gamma)$ in each subdomain, one has a problem representative for the entire class. All are contact equivalent [Golubitsky & Schaeffer, 1985]. Solving the chosen problem, one can cheaply study the properties of the entire class. Hence only few problems need be solved in case the bifurcation curves are calculated, and costs are saved significantly. Calculating bifurcation curves (or bifurcation surfaces) is a major effort in parameter engineering. Branching systems have been used for this purpose since [Seydel, 1979a].

9.     Other methods of computational bifurcation

The methods for the ODE boundary-value problem (11) allow to calculate Turing bifurcation curves. Singularities of higher order can also be calculated by branching systems. Such systems involve even more equations than the basic branching system (5). For instance, the extended system for a hysteresis point involves 3n+3 scalar equations [Roose & Piessens, 1985],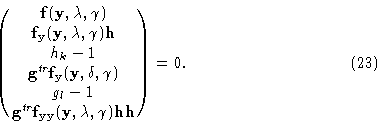

$$\pmatrix{{\bf f}({\bf y},\lambda,\gamma)\cr {\bf f}_{\bf y}(... ... y}}({\bf y},\lambda ,\gamma ){\bf h}{\bf h}} = \00 .\eqno(23)$$

The branching system (5) is a subset of Eq.(23). The last component in Eq.(23) is equivalent to $({\bf y}_0,\lambda_0)$ being a point of inflection. The involved left eigenvector ${\bf g}$ is defined by a subsystem, in analogy to Eq.(5). General procedures for calculating singularities were discussed in [Beyn, 1984], [Kunkel, 1988]. Another minimally extended system for simple bifurcation points was suggested in [Pönisch, 1985]. Procedures for the calculation of heteroclinic orbits were suggested in [Beyn, 1990], [Kuznetsov, 1990], [Friedman & Doedel, 1991]. For methods that determine the stability of periodic orbits refer to [Fairgrieve & Jepson, 1992], [Seydel, 1994]. For the stability check of stationary solutions of large systems an efficient procedure was suggested in [Neubert, 1993].

10.     Historical and further bibliographical remarks

Since numerical bifurcation has reached a level of some sophistication, it may be attempted to give a weighting review of some of the past research. For a long time, the numerical treatment of bifurcations was dominated by implementations of analytic methods. That is, computers were used as machines that amplified the analytical potential of researchers. Frequently, the applicability was restricted by the assumption that a branch ${\bf y}(\lambda)$ be known. Since the validity of analytical methods is often only local, such numerical approaches have not been convincing. Beginning in the late 1970s, numerical methods were suggested that broke with traditional approaches in that they were based on ideas not used previously for analytical treatment. A prototypical example for the new approaches is the branching system (5), which was pioneered in [Seydel, 1977, 1979a]. This approach makes use of the ability to solve complex nonlinear systems of equations iteratively, which can not be done with analytical methods. Following these lines, also the computation of emanating solutions can dispense with traditional analytical methods of calculating emanating solutions only locally.

Many papers have been devoted to the finite-dimensional situation of Eq.(1) which requires ``only" linear algebra. An influencial paper was [Keller, 1977]. The methods of [Seydel, 1977, 1979a] including the basic branching system were first formulated for the more difficult infinite-dimensional case of boundary-value problems, and later simplified to the finite-dimensional case of Eq.(1) [Seydel, 1979c]. The idea of regularization due to [Moore, 1980] (see Eq.(8)), and the attempt to set up minimal extended systems have further inspired the field. Many of the related papers have been quoted above. Today, for most bifurcation points a defining system is available. The notion of bifurcation test functions, which has found some recent interest, goes back to [Seydel, 1977, 1979].

In the past years, several software packs devoted to nonlinear computation have been developed. Here we do not attempt to present a review. A frequently used and successful package is AUTO due to Doedel, for references see [Doedel et al., 1991]. Most figures of WOB were calculated by means of BIFPACK [Seydel, 1997].

References

Allgower, E.L., Böhmer, K. & Golubitsky, M. [1992] Bifurcation and Symmetry (Birkhäuser, Basel) ISNM 104.

Allgower, E.L., Georg, K. & Miranda, R. (eds.) [1993] Exploiting Symmetry in Applied and Numerical Analysis (Amer. Math. Soc., Providence).

Beyn, W.-J. [1984] ``Defining equations for singular solutions and numerical applications," in Numerical Methods for Bifurcation Problems. Proceedings of a Conference in Dortmund, eds. Küpper, T., Mittelmann, H.D. & Weber, H. (Birkhäuser, Basel) ISNM 70.

Beyn, W.-J. [1990] ``The Numerical Computation of Connecting Orbits in Dynamical Systems,'' IMA J. Numer. Anal. 9, 379-405.

Doedel, E.J. [1997] ``Nonlinear numerics," Int. J. Bifurcation and Chaos 7.

Doedel, E.J., Keller, H.B. & Kernevez, J.P. [1991] ``Numerical analysis and control of bifurcation problems," Part I, Int. J. Bifurcation and Chaos 1 493-520; Part II, Int. J. Bifurcation and Chaos 1 745-772.

Fairgrieve, T.F. & Jepson, A.D. [1992] ``O.K. Floquet multipliers," SIAM J. Numer. Anal. 28, 1446-1462.

Friedman, M.J. & Doedel, E.J. [1991] ``Numerical computation and continuation of invariant manifolds connecting fixed points," SIAM J. Numer. Anal. 28, 789-808.

Golubitsky, M. & Schaeffer, D.G. [1985] Singularities and Groups in Bifurcation Theory. Vol.1 (Springer, New York).

Griewank, A. & Reddien, G.W. [1983] ``The calculation of Hopf bifurcation points by a direct method," IMA J. Numer. Anal. 3, 295-303.

Griewank, A. & Reddien, G.W. [1984] ``Characterization and computation of generalized turning points," SIAM J. Numer. Anal. 21, 176-185.

Holodniok, M. & Kubícek, M. [1984] ``DERPER--an algorithm for the continuation of periodic solutions in ordinary differential equations," J. Comput. Phys. 55, 254-267.

Keller, H.B. [1977] `` Numerical solution of bifurcation and nonlinear eigenvalue problems," in Applications of Bifurcation Theory, ed. Rabinowitz, P.H. (Academic Press, New York).

Kunkel, P. [1988] ``Quadratically convergent methods for the computation of unfolded singularities," SIAM J. Numer. Anal. 25, 1392-1408.

Kuznetsov, Yu. A. [1990] ``Computation of invariant manifold bifurcations," in, Continuation and Bifurcations, eds. Roose, D., et al. (Kluwer Academic Publishers) 183-195.

Moore, G. [1980] ``The numerical treatment of non-trivial bifurcation points," Numer. Funct. Anal. Optim. 2, 441-472.

Moore, G. & Spence, A. [1980] `` The calculation of turning points of nonlinear equations," SIAM J. Numer. Anal. 17, 567-576.

Neubert, R. [1993] ``Predictor-corrector techniques for detecting Hopf bifurcation points," Int. J. Bifurcation and Chaos 3, 1311-1318.

Pönisch, G. [1985] ``Computing simple bifurcation points using a minimally extended system of nonlinear equations," Computing 35, 277-294.

Reithmeier, E. [1991] Periodic Solutions of Nonlinear Dynamical Systems (Springer, Berlin).

Roose, D. [1985] ``An algorithm for the computation of Hopf bifurcation points in comparison with other methods," J. Comput. Appl. Math. 12&13, 517-529.

Roose, D. & Piessens, R. [1985] ``Numerical computation of nonsimple turning points and cusps," Numer. Math. 46, 189-211.

Seydel, R. [1977] ``Numerische Berechnung von Verzweigungen bei gewöhnlichen Differentialgleichungen," Ph.D. thesis. Report TUM 7736, Mathem. Institut, Technical Univ. Munich.

Seydel, R. [1979a] ``Numerical computation of branch points in ordinary differential equations," Numer. Math. 32, 51-68.

Seydel, R. [1979b] ``Numerical computation of primary bifurcation points in ordinary differential equations," in Constructive Methods for Nonlinear Boundary Value Problems and Nonlinear Oscillations. Proceedings of a Conference in Oberwolfach 1978, eds. Albrecht, J., Collatz, L. & Kirchgässner, K. (Birkhäuser, Basel) ISNM 48, 161-169.

Seydel, R. [1979c] ``Numerical computation of branch points in nonlinear equations," Numer. Math. 33, 339-352.

Seydel, R. [1981] ``Numerical computation of periodic orbits that bifurcate from stationary solutions of ordinary differential equations," Appl. Math. Comput. 9, 257-271.

Seydel, R. [1983] ``Branch switching in bifurcation problems of ordinary differential equations," Numer. Math. 41, 93-116.

Seydel, R. [1994] Practical Bifurcation and Stability Analysis. From Equilibrium to Chaos. Second Edition. Springer Interdisciplinary Applied Mathematics, Vol. 5. (Springer, New York).

Seydel, R. [1997] ``BIFPACK--a program package for continuation, bifurcation and stability analysis," (First version: Buffalo 1983, Current version 3.2, Ulm).

Seydel, R. [1997a] ``On a Class of Bifurcation Test Functions,''Chaos, Solitons & Fractals 8, 851-855.

Werner, B. & Spence, A. [1984] ``The computation of symmetry-breaking bifurcation points," SIAM J. Numer. Anal. 21, 388-399.

Postscript-File for better printing results:

This Tutorial