As seen in Tutorial 2, solutions of parameterized equations form continua, which are called branches. The decisive solutions where something ``happens'' are bifurcations. At these points, the stability may be lost, or the structure of the state may change drastically. Bifurcations have a qualitative flavor whereas the branches represent quantitative elements. A particular example may have a few bifurcation points, but it has an infinite number of solutions, at least one for each parameter value. Accordingly, the bulk of computations is the computation of the branches. The effort devoted to bifurcations is a relatively small fraction of the total expenses. Branches and bifurcations must be computed both. The resulting bifurcation diagram is the signature of the problem. This Tutorial 3 is devoted to the computation of the branches. The calculation of bifurcations is discussed in Tutorial 4. We shall concentrate on basic principles.

1. Predictor-corrector approach
The procedure will be studied on the formally simple problem
The first three of these four items can be chosen independently
of each other. But the step-length control must match the
predictor, the corrector, and the underlying parameterization.
All of the four ingredients have a local nature -- that is, they should be valid for the step ![]() and may be changed for the next step.
and may be changed for the next step.
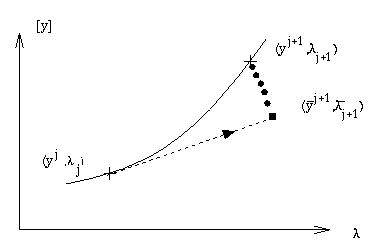
2. Predictors
Here we outline how the branch is locally approximated by a straight line. Taking the differential of both sides of Eq.(1), one obtains
Several continuation methods are based on tangent predictors. In these
methods the predictor point (initial approximation) for
![]() is
is
An alternative to the tangent is the secant
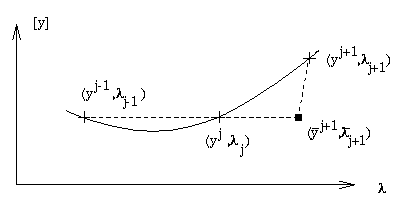
3. Parameterizations
The next step is to introduce a local measure along the branch. That is, the current part of the curve is ``parameterized." Terms like ``next" or ``previous" solution are quantified by introducing a parameterization. The most obvious parameter is the control variable
Curves such as solution branches of Eq.(1) can be parameterized by curve parameters. A general curve parameter, call it ![]() ,
may have
a geometrical rather than a physical meaning. A parameterization by
,
may have
a geometrical rather than a physical meaning. A parameterization by ![]() means that solutions of
means that solutions of
![]() depend at least locally on
depend at least locally on ![]() :
:
![]() For a particular value of
For a particular value of ![]() ,
the system
,
the system
![]() consists of n equations for the n+1 unknowns
consists of n equations for the n+1 unknowns
![]() .
If the
parameterization is established by one additional scalar equation,
.
If the
parameterization is established by one additional scalar equation,
![]() ,
one can formulate an extended system
,
one can formulate an extended system
The parameterizing equation
![]() is
attached to the given system of Eq.(1). The resulting system (6) is a general equation on which general software of numerical analysis is applicable. We call the chosen software SOLVER; in our setting this may be Newton's method. In this way, by calling SOLVER for Eq.(6), the desired
parameterization is imposed on Eq.(1) automatically. Alternatively,
one can apply the Newton method to Eq.(1) and impose an
appropriate side condition on the iteration. This
latter approach will be described in Section 4. The
formulation in Eq.(6) has the advantage of not being tied to a special version of a Newton method. Any modification or other iteration method for solving equations can be applied to solve Eq.(6).
is
attached to the given system of Eq.(1). The resulting system (6) is a general equation on which general software of numerical analysis is applicable. We call the chosen software SOLVER; in our setting this may be Newton's method. In this way, by calling SOLVER for Eq.(6), the desired
parameterization is imposed on Eq.(1) automatically. Alternatively,
one can apply the Newton method to Eq.(1) and impose an
appropriate side condition on the iteration. This
latter approach will be described in Section 4. The
formulation in Eq.(6) has the advantage of not being tied to a special version of a Newton method. Any modification or other iteration method for solving equations can be applied to solve Eq.(6).
A classical example of a curve parameter is the arclength s--that is,
![]() The arclength s has a global meaning. It satisfies both the linear system
The arclength s has a global meaning. It satisfies both the linear system
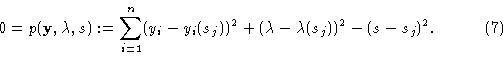
Another important way to parameterize a branch is to admit any of the components yi
![]() as a parameter, including
as a parameter, including
![]() .
This local parameterization leads to the
parameterizing equation
.
This local parameterization leads to the
parameterizing equation
It is easy to find a suitable index k and parameter
value ![]() .
A continuation algorithm based on tangent
predictors determines k such that
.
A continuation algorithm based on tangent
predictors determines k such that
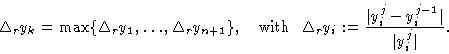
After an index k is fixed, a suitable parameter
value ![]() must be determined. A value of
must be determined. A value of ![]() depends on the
index k, on the location of the current solution on the branch (i.e.,
on j), and on the desired step size
depends on the
index k, on the location of the current solution on the branch (i.e.,
on j), and on the desired step size ![]() ,
,
The local parameterization
concept can be generalized to a continuation that involves
qualitative aspects. For example, a continuation by asymmetry is
furnished by
4. Correctors
In this section, we discuss how to solve Eq.(1) iteratively, starting from the predictor
Conceptual differences
among various parameterizations are not significant. In a practical
implementation, however, differences become substantial. Equations (6) and (10) can be solved without requiring specific
software. Alternatively, the block structure can be exploited; available decompositions of
![]() can be used for the decomposition of
can be used for the decomposition of
![]() .
.
5. Step controls
In simple problems the principles introduced above may work effectively without a step-length control. That is, constant step lengths are taken throughout. If the step size is small enough, such a step strategy may be successful for a wide range of problems. But such results are often obtained in an inefficient manner, involving too many steps along ``flat" branches. The step length should be adapted to the actual convergence behavior. Because step controls must meet the features of the underlying combination predictor/parameterization/corrector, step-length algorithms are specifically designed.
Step controls can be based on estimates of the
convergence quality of the corrector iteration. Such methods require a kind of absolute convergence measure to decide what is ``fast," or ``slow." A basic criterion for scaling step-length
algorithms can be based on the observation that the total amount of work
involved in a continuation depends on the average step length in
a somewhat convex manner: The continuation is expensive both for
very short steps (too many steps) and for very large steps (slow
or no convergence of correctors). The costs of a continuation
are moderate for a certain medium step length, which is related to an
optimal number
![]() of iterations of a corrector. This
number depends on the type of corrector and on the prescribed error
tolerance
of iterations of a corrector. This
number depends on the type of corrector and on the prescribed error
tolerance ![]() .
For example, with quasi-Newton correctors and
.
For example, with quasi-Newton correctors and
![]() the optimal number is
the optimal number is
![]() The aim is to adjust the step size so that each
continuation step needs about
The aim is to adjust the step size so that each
continuation step needs about
![]() corrector iterations.
Let Nj denote the number of iterations needed to approximate the
previous continuation step. Then a simple strategy is to reduce
the step size in case
corrector iterations.
Let Nj denote the number of iterations needed to approximate the
previous continuation step. Then a simple strategy is to reduce
the step size in case
![]() and to increase the step
size in case
and to increase the step
size in case
![]() .
This can be done, for example, by
updating the previous step size by multiplication with the factor
.
This can be done, for example, by
updating the previous step size by multiplication with the factor
6. Historical and bibliographical remarks on continuation
We conclude the section by adding some notes about the development of the continuation subject. In the 1960s, early papers suggesting basic ideas were [Haselgrove, 1961], [Klopfenstein, 1961], [Deist & Sefor, 1967]. One special aspect of continuation is homotopy, a strategy to facilitate the solution of a ``difficult" problem
In the 1970s, the interest shifted towards more algorithmic issues such as step length control, and to the calculation of general branches. Basic methods have been explained in this tutorial. Pseudo arclength was advocated by [Riks, 1972], [Keller, 1977], and local parameterization by [Rheinboldt, 1980], [Seydel, 1979b], [Seydel, 1984]. The updating of step lengths by orientation on an optimal number of steps
![]() was suggested in [Seydel, 1977], [Seydel, 1984]. Such a strategy has become a core of many step length algorithms. It has turned out that simple continuation principles work well on most problems. For specific methods on continuation see [Menzel & Schwetlick, 1978], [Den Heijer & Rheinboldt, 1981], [Rheinboldt & Burkardt, 1983], [Deuflhard et al., 1987]; further references can be found in [Seydel, 1994]. Technical issues of continuation are discussed in [Rheinboldt et al., 1990]. An account of simplicial methods is included in [Allgower & Georg, 1990].
was suggested in [Seydel, 1977], [Seydel, 1984]. Such a strategy has become a core of many step length algorithms. It has turned out that simple continuation principles work well on most problems. For specific methods on continuation see [Menzel & Schwetlick, 1978], [Den Heijer & Rheinboldt, 1981], [Rheinboldt & Burkardt, 1983], [Deuflhard et al., 1987]; further references can be found in [Seydel, 1994]. Technical issues of continuation are discussed in [Rheinboldt et al., 1990]. An account of simplicial methods is included in [Allgower & Georg, 1990].
References
Allgower, E.L. & Georg, K. [1990] Numerical Continuation Methods (Springer, Berlin).
Deist, F.H. & Sefor, L. [1967] ``Solution of systems of non-linear equations by parameter variation," Computer J. 10, 78-82.
Den Heijer, C. & Rheinboldt, W.C. [1981] ``On steplength algorithms for a class of continuation methods," SIAM J. Numer. Anal. 18, 925-948.
Deuflhard, P., Fiedler , B. & Kunkel, P. [1987] ``Efficient numerical path following beyond critical points," SIAM J. Numer. Anal. 24, 912-927.
Haselgrove, C.B. [1961] ``The solution of nonlinear equations and of differential equations with two-point boundary conditions," Comput. J. 4, 255-259.
Keller, H.B. [1977] `` Numerical solution of bifurcation and nonlinear eigenvalue problems," in Applications of Bifurcation Theory, ed. Rabinowitz, P.H. (Academic Press, New York).
Klopfenstein, R.W. [1961] `` Zeros of nonlinear functions," J. ACM 8, 366-373.
Menzel, R. & Schwetlick, H. [1978] ``Zur Lösung parameterabhängiger nichtlinearer Gleichungen mit singulären Jacobi-Matrizen," Numer. Math. 30, 65-79.
Rheinboldt, W.C. [1980] ``Solution fields of nonlinear equations and continuation methods," SIAM J. Numer. Anal. 17, 221-237.
Rheinboldt, W.C. & v. Burkardt, J. [1983] ``A locally parametrized continuation process," ACM Trans. of Math. Software 9, 215-235.
Rheinboldt, W.C., Roose, D. & Seydel, R. [1990] ``Aspects of continuation software," in Continuation and Bifurcations: Numerical Techniques and Applications, eds. Roose, D. et al. (Kluwer Academics Publisher) 261-268.
Riks, E. [1972] ``The application of Newton's method to the problem of elastic stability," Trans. ASME, J. Appl. Mech. 1060-1065.
Seydel, R. [1977] ``Numerische Berechnung von Verzweigungen bei gewöhnlichen Differentialgleichungen," Ph.D. thesis. Report TUM 7736, Mathem. Institut, Technical Univ. Munich.
Seydel, R. [1979b] ``Numerical computation of primary bifurcation points in ordinary differential equations," in Constructive Methods for Nonlinear Boundary Value Problems and Nonlinear Oscillations. Proceedings of a Conference in Oberwolfach 1978, eds. Albrecht, J., Collatz, L. & Kirchgässner, K. (Birkhäuser, Basel) ISNM 48, 161-169.
Seydel, R. [1984] ``A continuation algorithm with step control," in Numerical Methods for Bifurcation Problems. Proceedings of a Conference in Dortmund, 1983, eds. Küpper, T., Mittelmann, H.D. & Weber, H. (Birkhäuser, Basel) ISNM 70, 480-494.
Seydel, R. [1994] Practical Bifurcation and Stability Analysis. From Equilibrium to Chaos. Second Edition. Springer Interdisciplinary Applied Mathematics, Vol. 5. (Springer, New York).