Model of student migration

Original source (Postscript-File): J. Scheurle, R. Seydel: A Model of Student Migration. to appear in Int. J. Bifurcation and Chaos


Two fixed points are

\begin{displaymath}y_1={\lambda\over d_1},\quad y_2=0\end{displaymath}

and

\begin{displaymath}y_1={\beta+d_2\over a},\quad y_2={1\over d_2}\left(\lambda-{d_1\over a}(\beta +d_2)\right)\end{displaymath}

They are connected by a bifurcation with

\begin{displaymath}\lambda a=d_1(\beta +d_2).\end{displaymath}

It is easy to show that the fixed point with y2=0 is stable for

\begin{displaymath}a\lambda <d_1(\beta+d_2).\end{displaymath}

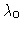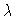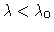This defines a threshold value $\lambda_0$ of the number $\lambda$ of entering freshmen, such that for $\lambda <\lambda_0$ the option 2 has no students. The bound is not touched for

\begin{displaymath}d_1(\beta +d_2)<a\lambda <d_1(\beta +d_2)+\gamma d_2.\end{displaymath}


Figure 1
Phase-diagram of the (y1j, y2j)-values for j=0,1,...,40, 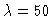$\lambda =50$, a=0.002.

Postscript-Files for better printing results:

This document
Figure 1