Logo

Brusselator with Two Coupled Cells

The equations reflect the Brusselator kinetics in each cell. There are two kinds of reactions. For a homogeneous reaction, both cells exhibit identical behavior,

\begin{displaymath}y_1(t) = y_3(t), \ \ y_2(t) = y_4(t) \ \ \hbox { for all } t.\end{displaymath}

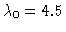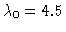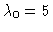The reaction is said to be inhomogeneous if this identity does not hold. The branching behavior is depicted in Figure 1. The branch indicated by a full line and the branch that bifurcates off at $\lambda_0=4.5$ (dashed lines) consist of stationary solutions. At $\lambda_0=4.5$, the stability is exchanged. All the other branches consist of periodic orbits. For the value $\lambda_0=5$, there is a Hopf bifurcation into periodic homogeneous orbits. 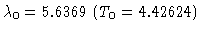First, the emerging branch is unstable; it gains stability at $\lambda_0 =5.6369\ (T_0=4.42624)$ via a subcritical pitchfork bifurcation. 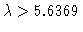That is, for $\lambda >5.6369$ there are stable homogeneous oscillations, which are ``encircled" by unstable inhomogeneous orbits. 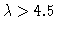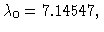The two branches of stationary inhomogeneous solutions, which exist for $\lambda >4.5$, lose their stability at the two Hopf bifurcation points with $\lambda_0=7.14547,$ T0=2.88882.

A remarkable part of the solutions is the Hopf bifurcation at 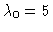$\lambda_0=5$. Because all of the solutions merging in the bifurcation point

\begin{displaymath}y_1 = y_3 = 2, \ \ y_2 = y_4 = 2.5 ,\ \lambda =5\end{displaymath}

are homogeneous, the coupling terms vanish; the equations of the two cells decouple. Consequently, the same solutions can be calculated by solving only the subsystem of the first two equations (n=2). In this way, both the homogeneous equilibria and the homogeneous oscillations are obtained. However, the stability behavior is different. 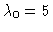The bifurcations into inhomogeneous solutions do not exist for the reduced system, and there is an exchange of stability at $\lambda_0=5$. This shows that by the process of coupling two identical cells the stability behavior can change drastically. In particular, the homogeneous orbits in the range

\begin{displaymath}5 < \lambda < 5.6369\end{displaymath}

lose stability, caused by the onset of additional bifurcations. This serves as an example for the phenomenon that relaxing a restriction can enrich the bifurcation behavior. Concerning the underlying ``spaces" of admissible functions, distinguish between the space of smooth vector functions with independent components and the small subspace of homogeneous functions satisfying y1=y3, y2=y4.
Figure 1
Two-cells Brusselator, branching diagram y2(0) versus 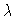$\lambda$.

Postscript-Files for better printing results:

This Example
Figure 1