WOB Examples

Steady-State Brusselator with Diffusion

The system is the same as the one in WOBexa1. Scaling the independent variable according to t:=x/L leads to the system of four ODEs of the first order

$\begin{displaymath}y'_1 & = y_2 \cr\end{displaymath}$

$\begin{displaymath}y'_2 & = - \lambda [A+y^2_1 y_3-(B+1)y_1 ]/D_1 \cr\end{displaymath}$

$\begin{displaymath}y'_3 & = y_4 \cr\end{displaymath}$

$\begin{displaymath}y'_4 & = - \lambda [By_1 -y^2_1 y_3 ]/D_2 \cr\end{displaymath}$

with boundary conditions

$\begin{displaymath}y_1 (0) = y_1 (1) = A, \ \ y_3 (0) = y_3 (1) = B/A. \end{displaymath}$

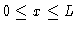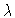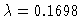The ordinary differential equations describe the spatial dependence of the two chemicals X and Y along a reactor with length L, $0\le x\le L$ . This Brusselator model equation has a great number of solutions ; some are represented in the branching diagram of Figure 1, which depicts y₂(0)=X'(0) versus $\lambda$ . One nontrivial bifurcation point is found for $\lambda=0.1698$ , y₂(0)=6.275.

Figure 1
Bifurcation diagram X'(0) versus 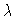$\lambda$

Postscript-Files for better printing results:

This Example
Figure 1