Steady-State Brusselator with Diffusion

exb4
Variables and parameters:

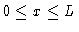x: spatial coordinate, $0\leq x\leq L$

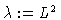L: reactor length, $\lambda:=L^2$ bifurcation parameter

X,Y: chemicals

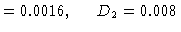D1 $=0.0016, \hskip 0.5 true cm D_2 =0.008$, diffusion constants

A =2, B=4.6


Differential equations:

\begin{displaymath}0 & = A + X^2 Y - BX - X + D_1 {\partial^2 X \over \partial x^2}\cr\end{displaymath}


\begin{displaymath}0 & = BX - X^2 Y + D_2 {\partial^2 Y \over \partial x^2}\cr\end{displaymath}



Boundary conditions

\begin{displaymath}X & = A \hskip 1.4 true cm \hbox { for } x = 0,\ x = L \cr\end{displaymath}


\begin{displaymath}Y & = B/A \hskip 0.9 true cm \hbox { for } x = 0, \ x = L \cr\end{displaymath}




Comments

Figure 1
Bifurcation diagram X'(0) versus 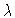$\lambda$

Postscript-Files for better printing results:

This Example
Figure 1