WOB Examples

Forced Duffing Oscillator

Derivation of the equation:

Duffing equations are used to model certain mechanical or electrical oscillators. One frequently mentioned derivation as a one-mode approximation of the deflections $v(x,t)=u(t)\sin\pi x$ of a symmetric beam modelled by

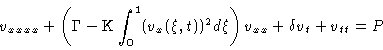
$\begin{displaymath}v_{xxxx} + \left(\Gamma - {\rm K} \int ^1_0 (v_x (\xi,t))^2 d \xi\right) v_{xx} + \delta v_t + v_{tt} =P\end{displaymath}$

with

$\begin{displaymath}P(x,t) &= \gamma \cos \omega t \sin \pi x ,\quad 0\leq x\leq 1, \cr \end{displaymath}$

$\begin{displaymath}\Gamma &= \pi^2 + 0.2 \pi^{-2}, \ \ K = 16 \pi^{-4} /15, \cr \end{displaymath}$

$\begin{displaymath}\gamma& = 0.4, \ \ \delta=0.04\cr \end{displaymath}$

is summarized in [R. Seydel: Practical Bifurcation and Stability Analysis. From Equilibrium to Chaos. Second Edition. Springer Interdisciplinary Applied Mathematics 1994.]

It is an instructive exercise to consider the case $\gamma=0$ (no driving force) with the compressive force $\Gamma$ as bifurcation parameter. For $\Gamma=\pi^2$ there is a pitchfork bifurcation. At this value of Euler's first buckling load the underlying beam starts to bend. Up to symmetry, one stable equilibrium exists for each $\Gamma >\pi^2$ . This is satisfied by our parameters.

First-order System:

The harmonic forcing term $0.4 \cos\omega t$ on the right-hand side provokes a response of the system (beam, electric current). The harmonic oscillations obey the boundary conditions

$\begin{displaymath}u(0) = u(T), \ \ \dot u(0) = \dot u(T).\end{displaymath}$

Because the period T varies with $\omega$ , the integration interval $0\le t\le T$ must be adapted whenever $\omega$ is changed. This is inconvenient when nodes of a numerical solution procedure must also be adapted, so we transform the integration interval to unit length, thereby shifting the dependence on $\omega$ to the right-hand side of the differential equation. The normalized time $\tilde t$ satisfies

$\begin{displaymath}T\tilde t = t, \ \ 0\le \tilde t\le 1. \end{displaymath}$

The transformation

$\begin{displaymath}y_1 (\tilde t): = u(t),\ \ y_2 (\tilde t): = \dot u(t) \end{displaymath}$

leads to the first-order system

$\begin{displaymath}y'_1 & = Ty_2 ,\cr \end{displaymath}$

$\begin{displaymath}y'_2 & = T(-0.04y_2 + 0.2y_1 - 8y^3_1 /15 + 0.4 \cos 2 \pi \tilde t)\cr \end{displaymath}$

with boundary conditions

$\begin{displaymath}y_1 (0) - y_1 (1) & = 0 ,\cr \end{displaymath}$

$\begin{displaymath}y_2 (0) - y_2 (1) & = 0. \cr\end{displaymath}$

Redefining the normalized time by t, we obtain a boundary-value problem of a standard form. With $y_3 :=\omega$ , the corresponding extended system is

$\begin{displaymath}y'_1 & = 2\pi y_2 /y_3 ,\cr \end{displaymath}$

$\begin{displaymath}y'_2 & = 2\pi (-0.04y_2 +0.2y_1 -8y^3_1 /15+0.4 \cos 2\pi t)/y_3 ,\cr \end{displaymath}$

$\begin{displaymath}y'_3 & = 0 ,\cr \end{displaymath}$

$\begin{displaymath}& {\hskip 2.8 true cm} y_1 (0) - y_1 (1) = 0 , \cr \end{displaymath}$

$\begin{displaymath}& {\hskip 2.8 true cm} y_2 (0) - y_2 (1) = 0 ,\cr \end{displaymath}$

$\begin{displaymath}& {\hskip 2.8 true cm} y_k (0) - \eta = 0 .\cr \end{displaymath}$

Bifurcations:

A main part of the bifurcation diagram is shown in Figures 1, 2. The branching behavior is rich for small values of $\omega$ . As Figure 3 shows, there are many branches, turning points, and bifurcation points for values of the parameter $\omega <0.5.$ The solid curve in this branching diagram represents oscillations, with phase diagrams being symmetric with respect to the origin as in Figure 4. For decreasing $\omega$ , each loop of this ``main" branch attaches a further wiggle to the oscillation. The wiggles indicate that the small-amplitude oscillation around any of the stable equilibria takes much time to collect enough energy before a transition to the other attracting basin is possible; compare the phase diagram in Figure 4 and the time dependence in Figure 5 $(\omega =0.053)$ . At first glance, the many wiggles might give the impression that such solutions are not harmonic; but they do have period T. Each of the closed branches in Figure 3 (dashed and dotted curves) is attached to the main branch via two pitchfork bifurcations. Accordingly, the phase diagrams of these ``secondary" branches are asymmetric with respect to the origin; Figure 6 shows one such phase plot. The closed branch in Figure 7 (drawn in Figure 3 in a dashed line) appears to have sharp corners, and one might expect difficulties in tracing this particular branch. The plotted behavior refers only to the dependence y₁ (0) versus $\lambda$ ; the corresponding graph of y₂ (0) behaves more smoothly (Figure 8).

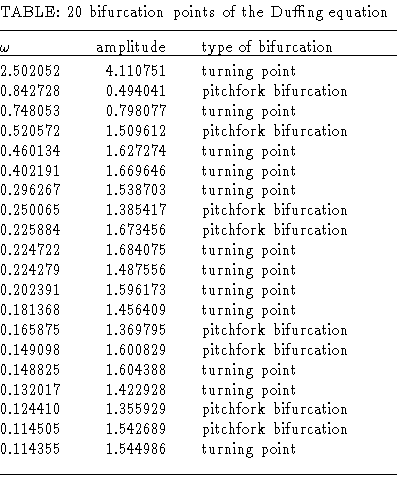
The table includes 20 bifurcation points of the above Duffing equation with accurate values of the amplitude. The above Duffing equation also exhibits subharmonic oscillations; then the period of the system is an integral multiple of the period of the external frequency. Branches of subharmonic solutions bifurcate from the harmonic solutions (not listed in the table). Stability, and period doubling scenarios have been calculated by K. Riedel (Ulm 1996). For example, a period doubling cascade starts at $0.88846\ (u(0)=-0.66)$ .

$\begin{displaymath}% latex2html id marker 104 \vbox {\halign {$ ...$

Chaotic solutions:

For a range of $\omega$ -values ther exist chaotic attractors. One such attractor is illustrated by the Poincaré map / stroboscopic map $\left(u(t_k),\dot u(t_k)\right)$ , $t_k={2\pi\over\omega}$ , k=1,2,...,8000, $\omega=0.2$ , $u(0)=\dot u(0)=0$ in Figure 9.