
Superconductivity Within a Slab
Original source of the model: F. Odeh: Existence and bifurcation theorems for the
Ginzburg-Landau equations. J. Math. Phys. 8 (1967) 2351-2356.
Solutions are summarized in the branching diagram in Figure 1.
A branch of asymmetric solutions branches off a
branch of symmetric solutions at a pitchfork bifurcation point.
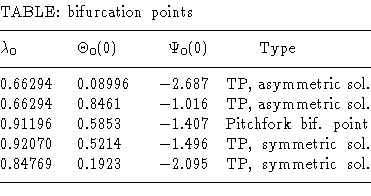
The data of the bifurcation point and four turning points (TP)
are listed in the Table.
Investigation of the above boundary-value problem reveals that it
supports symmetry. To see this, define
and realize that the signs are the same after differentiating
twice with respect to x. Hence,
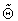 and
and
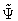 satisfy
the differential
equations if
satisfy
the differential
equations if 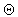 and
and 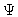 do. Analyzing the boundary
conditions, as, for example,
do. Analyzing the boundary
conditions, as, for example,
shows that
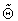 and
and
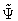 satisfy the boundary
conditions. Hence, the
equation supports even
satisfy the boundary
conditions. Hence, the
equation supports even 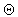 and odd
and odd 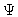 .
This does not imply
that solutions must be even or odd. In fact, the equation
has asymmetric solutions. See the solution in Figure 2,
which depicts both the solutions
.
This does not imply
that solutions must be even or odd. In fact, the equation
has asymmetric solutions. See the solution in Figure 2,
which depicts both the solutions
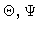 and
and
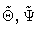 for the parameter value
for the parameter value
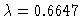 .
.
In order to calculate solutions, we rewrite the
boundary-value problem as a first-order system. Denoting
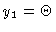 ,
,
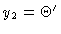 ,
,
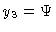 ,
and
,
and
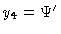 yields
yields
The
solution profiles of the bifurcation point are
shown in Figures 4 and 5;
notice the symmetries. This bifurcation point is straddled
between the two turning points with asymmetric solutions, which
are depicted in Figures 2 and 3. Compare the figures to see how
this straddling becomes evident in the solution profiles.
Figure 1
Bifurcation diagram 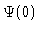 versus
versus 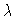 .
Two branches intersecting in a pitchfork bifurcation.
.
Two branches intersecting in a pitchfork bifurcation.
Figure 2
Two antisymmetric solutions 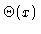 for
for
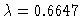 .
.
Figure 3
Two antisymmetric solutions 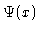 for
for
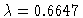 .
.
Figure 4
Symmetric solution 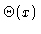 for
for
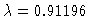 .
.
Figure 5
Symmetric solution 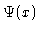 for
for
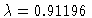 .
.
Postscript-Files for better printing results:
This Example
Figure 1
Figure 2
Figure 3
Figure 4
Figure 5

![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() yields
yields
![]() for
for
![]() .
.
![]() for
for
![]() .
.
![]() for
for
![]() .
.
![]() for
for
![]() .
.