
Three Coupled Cells with Brusselator Reaction
The trimolecular reaction
was introduced in
P. Glansdorff, I. Prigogine: Thermodynamic Theory of
Structure, Stability and Fluctuations. Wiley-Interscience, London 1971.
The concentrations of the chemicals A, B, D, E
are assumed to remain at a constant level. Taking all direct
kinetic constants equal to one, and neglecting the reverse
processes, the reaction is described by the differential
equations
The variable x measures the length of the reactor. In
what follows, we shall concentrate on the kinetic equations--that is,
we neglect the diffusion terms
(D1 =D2 =0).
Here we consider the steady-state situation
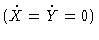 in
three connected reaction cells with coefficients A=2, B=6.
y1 and y2 stand for X and Y in the first cell, and so on.
in
three connected reaction cells with coefficients A=2, B=6.
y1 and y2 stand for X and Y in the first cell, and so on.
An inspection of the equations reveals that an exchange
yields the same equations. After a permutation of the order of
equations, we arrive back at the original equation. This process of
exchanging is described by the transformation
We realize that this transformation and the
equation written as
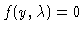 satisfy the equivariance condition
satisfy the equivariance condition
and
S2=I holds. That is, the equation is Z2 symmetric.
Hence, in this example, we expect pitchfork bifurcations
with symmetry breaking.
As an inspection of the equations shows,
there is a stationary solution for all 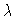 ,
,
For our choice of parameters this solution is given by
We restrict a numerical analysis to the parameter
range
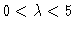 .
The resulting branching diagram is depicted
in Figure 1, and a detail for small values of
.
The resulting branching diagram is depicted
in Figure 1, and a detail for small values of 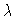 is shown in
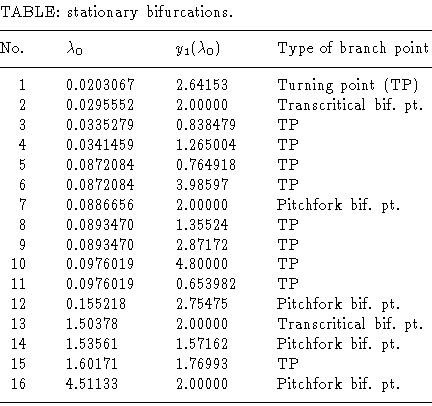
Figure 2. As these figures show, there are a great number of
turning points, pitchfork bifurcations, and transcritical
bifurcations. The branch points are listed in the Table
(rounded to six digits). In addition, Hopf bifurcations exist.
is shown in
Figure 2. As these figures show, there are a great number of
turning points, pitchfork bifurcations, and transcritical
bifurcations. The branch points are listed in the Table
(rounded to six digits). In addition, Hopf bifurcations exist.
Figure 3 condenses the bifurcation behavior in a qualitative way.
The nontrivial branches are connected with the trivial
branch via bifurcation points 2, 7, 13, 16. Because only
two are pitchfork bifurcations, the way
symmetries are broken or preserved is especially interesting.
The trivial branch reflects a ``higher" regularity than the
symmetry condition with S because
holds. In Figure 3, symmetric solutions with respect
to S are indicated by solid lines, and branches of
asymmetric solutions are dashed, or dotted. The symmetry defined by the
matrix S
is preserved at the transcritical bifurcation points 2 and
13, but at these points the regularity responsible for
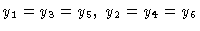 is broken. Symmetry breaking of the Z2 symmetry
takes place at the
pitchfork bifurcations 7, 12, 14, 16.
is broken. Symmetry breaking of the Z2 symmetry
takes place at the
pitchfork bifurcations 7, 12, 14, 16.
Figure 1
Bifurcation diagram y1 versus 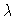 .
.
Figure 2
y1 versus 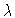 ,
detail of Figure 1.
,
detail of Figure 1.
Figure 3
Schematic bifurcation; for numbers of bifurcations see Table.
Postscript-Files for better printing results:
This Example
Figure 1
Figure 2
Figure 3

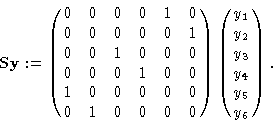
![]() ,
,
![]() ,
detail of Figure 1.
,
detail of Figure 1.